
 �輯��W������������������������{an}���ɣ�
�輯��W������������������������{an}���ɣ�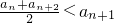 ���ڴ���ʵ��M��ʹan��M���� nΪ��������
���ڴ���ʵ��M��ʹan��M���� nΪ��������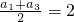 =a2��
=a2��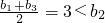 ��
��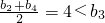 ��
��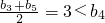 ��
��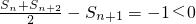 ����
����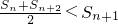 ��
��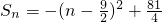 ����Sn�����ֵ��S4=S5=20����Sn��S4=20��
����Sn�����ֵ��S4=S5=20����Sn��S4=20�� ��
��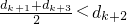 ����dk+3��dk+2+��dk+2-dk+1����dk+2��
����dk+3��dk+2+��dk+2-dk+1����dk+2�� ��������dk+2��dk+1+��dk+1-dk��=dk+1+��dk+1-M������Ϊdk=M���õ�dk+1��M����dk+2��dk+1������Ϊ
��������dk+2��dk+1+��dk+1-dk��=dk+1+��dk+1-M������Ϊdk=M���õ�dk+1��M����dk+2��dk+1������Ϊ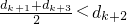 ���õ�dk+3��dk+2+��dk+2-dk+1����dk+2�������ɵ�֤��
���õ�dk+3��dk+2+��dk+2-dk+1����dk+2�������ɵ�֤��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 �輯��W������������������������{an}���ɣ�
�輯��W������������������������{an}���ɣ�| an+an+2 | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| an+an+2 |
| 2 |
| 1 |
| 4 |
| 7 |
| 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| an+an+2 |
| 2 |
| 2n+9 |
| 2n+11 |
| 4 |
| n |
| 1 |
| 2n |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������з�̨��2010�����һģ���ԣ���ѧ���� ���ͣ������
��14�֣��輯��W������������������������ ���ɣ�
���ɣ�
��
�ڴ���ʵ��M��ʹ ��nΪ��������
��n��������
��I����ֻ��5�����������
 ���������
�����ж����� �Ƿ�Ϊ����W��Ԫ�أ�
�Ƿ�Ϊ����W��Ԫ�أ�
��II���� �Ǹ���Ϊ���ĵȱ����У�
�Ǹ���Ϊ���ĵȱ����У� ����ǰn��ͣ�
����ǰn��ͣ� ֤������
֤������ ����д��M��ȡֵ��Χ��
����д��M��ȡֵ��Χ��
��III��������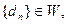 �Ҷ�����������M����СֵM0������
�Ҷ�����������M����СֵM0������ .
.
��֤������ ��������.
��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2010�걱���з�̨��������ѧ��һģ��ѧ���ģ����� ���ͣ������
��14�֣�
�輯��W������������������������ ���ɣ�
���ɣ�
��
�ڴ���ʵ��M��ʹ ��nΪ��������
��n��������
��I����ֻ��5�����������
 ���������
�����ж����� �Ƿ�Ϊ����W��Ԫ�أ�
�Ƿ�Ϊ����W��Ԫ�أ�
��II����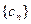 �ǵȲ����У�
�ǵȲ����У� ����ǰn��ͣ�
����ǰn��ͣ� ֤������
֤������ ����д��M��ȡֵ��Χ��
����д��M��ȡֵ��Χ��
��III�������� �Ҷ����������ij���M������������k��ʹ
�Ҷ����������ij���M������������k��ʹ
��֤��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com