
 );
); )
) ,∴yM=-
,∴yM=- ….(4分)
….(4分)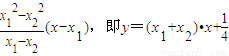
 )…(8分)
)…(8分)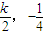 ),PQ:y=kx+
),PQ:y=kx+
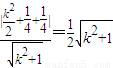
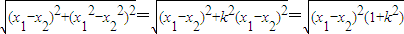
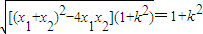
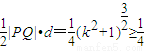 (此时k=0)…..(14分)
(此时k=0)…..(14分)

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010年广东省广州市番禺区高二下学期期中考试数学(文) 题型:解答题
(14分)已知抛物线C的顶点在原点,焦点为F(0,1),且过点A(2,t),
(1)求t的值;
(2)若点P、Q是抛物线C上两动点,且直线AP与AQ的斜率互为相反数,试问直线PQ的斜率是否为定值,若是,求出这个值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2010年广东省广州市番禺区高二下学期期中考试数学(理) 题型:解答题
(14分)已知抛物线C的顶点在原点,焦点为F(0,1),且过点A(2,t),
(1)求t的值;
(2)若点P、Q是抛物线C上两动点,且直线AP与AQ的斜率互为相反数,试问直线PQ的斜率是否为定值,若是,求出这个值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com