
ЁОЬтФПЁПФГжабЇГЄЦкМсГжЙсГЙвдШЫЮЊБОЃЌвђВФЪЉНЬЕФНЬг§РэФюЃЌУПФъЖМЛсдкаЃЮФЛЏНкЦкМфОйааЁАЪ§бЇЫибјФмСІВтЪдЁБКЭЁАгяЮФЫибјФмСІВтЪдЁБСНЯюВтЪдЃЌвдИјбЇЩњПЮЭтаЫШЄбЇЯАМАИЈЕМЬсЙЉВЮПМвРОнЃЎГЩМЈЗжЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮхИіЕШМЖЃЈЕШМЖ
ЮхИіЕШМЖЃЈЕШМЖ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЗжБ№ЖдгІ5ЗжЃЌ4ЗжЃЌ3ЗжЃЌ2ЗжЃЌ1ЗжЃЉЃЎФГАрбЇЩњСНПЦЕФПМЪдГЩМЈЕФЪ§ОнЭГМЦШчЭМЫљЪОЃЌЦфжаЁАгяЮФЫибјФмСІВтЪдЁБПЦФПЕФГЩМЈЮЊ
ЗжБ№ЖдгІ5ЗжЃЌ4ЗжЃЌ3ЗжЃЌ2ЗжЃЌ1ЗжЃЉЃЎФГАрбЇЩњСНПЦЕФПМЪдГЩМЈЕФЪ§ОнЭГМЦШчЭМЫљЪОЃЌЦфжаЁАгяЮФЫибјФмСІВтЪдЁБПЦФПЕФГЩМЈЮЊ![]() ЕФПМЩњга3ШЫЃЎ
ЕФПМЩњга3ШЫЃЎ
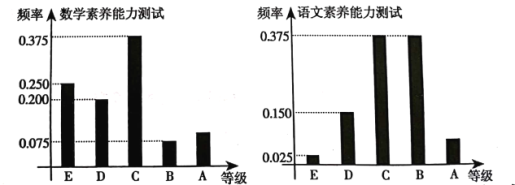
ЃЈ1ЃЉЧѓИУАрЁАЪ§бЇЫибјФмСІВтЪдЁБЕФПЦФПЦНОљЗжвдМАЁАЪ§бЇЫибјФмСІВтЪдЁБПЦФПГЩМЈЮЊ![]() ЕФШЫЪ§ЃЛ
ЕФШЫЪ§ЃЛ
ЃЈ2ЃЉШєИУАрЙВга9ШЫЕУЗжДѓгк7ЗжЃЌЦфжага2ШЫ10ЗжЃЌ3ШЫ9ЗжЃЌ4ШЫ8ЗжЃЎДгет9ШЫжаЫцЛњГщШЁШ§ШЫЃЌЩшШ§ШЫЕФГЩМЈжЎКЭЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉДгИУАрЕУЗжДѓгк7ЗжЕФ9ШЫжабЁ3ШЫМДМзЃЌввЃЌБћзщЖгВЮМгбЇаЃФкЕФЁАЪ§бЇЯоЪБНтЬтЬєеНШќЁБЃЎЙцдђЮЊЃКУПЖгЪзЯШХЩвЛУћЖгдБВЮМгЬєеНШќЃЌдкЯоЖЈЕФЪБМфЃЌШєИУЩњНтОіЮЪЬтЃЌМДЭХЖгЬєеНГЩЙІЃЌНсЪјЬєеНЃЛШєНтОіЮЪЬтЪЇАмЃЌдђХЩСэЭтвЛУћЖгдБЩЯШЅЬєеНЃЌжБжСХЩЭъЖгдБЮЊжЙЃЎЭЈЙ§бЕСЗЃЌвбжЊМзЃЌввЃЌБћЭЈЙ§ЬєеНШќЕФИХТЪЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЮЪвддѕбљЕФЯШКѓЫГађХЩГіЖгдБЃЌПЩЪЙЕУХЩГіЖгдБЪ§ФПЕФОљжЕДяЕНзюаЁЃПЃЈжЛашаДГіНсЙћЃЉ
ЃЌЮЪвддѕбљЕФЯШКѓЫГађХЩГіЖгдБЃЌПЩЪЙЕУХЩГіЖгдБЪ§ФПЕФОљжЕДяЕНзюаЁЃПЃЈжЛашаДГіНсЙћЃЉ
ЁОД№АИЁПЃЈ1ЃЉ2.575,4ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉввЃЌМзЃЌБћЃЎ
ЃЛЃЈ3ЃЉввЃЌМзЃЌБћЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЦЕТЪЗжВМжБЗНЭМЃЌжБНгЧѓМгШЈЦНОљЪ§ЃЌдйИљОнгяЮФЫибјФмСІВтЪдЮЊ![]() ЕФЦЕТЪКЭШЫЪ§ЕУГізмШЫЪ§ЃЌдйИљОнЁАЪ§бЇЫибјФмСІВтЪдЁБПЦФПЕФЦЕТЪМДПЩЕУНт.
ЕФЦЕТЪКЭШЫЪ§ЕУГізмШЫЪ§ЃЌдйИљОнЁАЪ§бЇЫибјФмСІВтЪдЁБПЦФПЕФЦЕТЪМДПЩЕУНт.
ЃЈ1ЃЉгЩЭМПЩжЊЃЌЪ§бЇЫибјФмСІВтЪдЮЊ![]() ЕФЦЕТЪЮЊ0.1ЃЌЙЪИУАрЁАЪ§бЇЫибјФмСІВтЪдЁБЕФПЦФПЦНОљЗжЮЊ
ЕФЦЕТЪЮЊ0.1ЃЌЙЪИУАрЁАЪ§бЇЫибјФмСІВтЪдЁБЕФПЦФПЦНОљЗжЮЊ![]() ЃЌ
ЃЌ
гяЮФЫибјФмСІВтЪдЮЊ![]() ЕФЦЕТЪЮЊ0.075ЃЌЙЪЖјИУАрга
ЕФЦЕТЪЮЊ0.075ЃЌЙЪЖјИУАрга![]() ШЫЃЎЁАЪ§бЇЫибјФмСІВтЪдЁБПЦФПГЩМЈЮЊ
ШЫЃЎЁАЪ§бЇЫибјФмСІВтЪдЁБПЦФПГЩМЈЮЊ![]() ЕФШЫЪ§
ЕФШЫЪ§![]() ЃЈШЫЃЉЃЎ
ЃЈШЫЃЉЃЎ
ЃЈ2ЃЉвРЬтЃК![]() ЕФШЁжЕПЩЮЊ29ЃЌ28ЃЌ27ЃЌ26ЃЌ25ЃЌ24ЃЎ
ЕФШЁжЕПЩЮЊ29ЃЌ28ЃЌ27ЃЌ26ЃЌ25ЃЌ24ЃЎ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]()
![]() ЃЎ
ЃЎ
ЃЈ3ЃЉввЃЌМзЃЌБћЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФРтзЖ![]() жаЃЌВрРт
жаЃЌВрРт![]() ДЙжБгкЕзУц
ДЙжБгкЕзУц![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЦНаагк
ЦНаагк![]() ЃЌ
ЃЌ![]() ЦНаагкУц
ЦНаагкУц![]() ЃЌ
ЃЌ![]() .
.
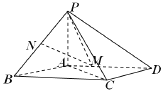
(1)Чѓ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
(2)ЧѓЖўУцНЧ![]() ЕФгрЯвжЕ.
ЕФгрЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкШ§РтжљABCЉA1B1C1жаЃЌВрУцABB1A1ЪЧСтаЮЃЌЧвCAЃНCB1ЃЎ
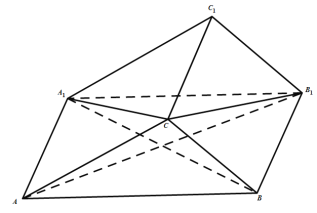
ЃЈ1ЃЉжЄУїЃКУцCBA1ЁЭУцCB1AЃЛ
ЃЈ2ЃЉШєЁЯBAA1ЃН60ЁуЃЌA1CЃНBCЃНBA1ЃЌЧѓЖўУцНЧCЉA1B1ЉC1ЕФгрЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌЦфжа
ЃЌЦфжа![]() .
.
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓжЄЃКЙ§дЕу
ЪБЃЌЧѓжЄЃКЙ§дЕу![]() ЧвгыЧњЯп
ЧвгыЧњЯп![]() ЯрЧаЕФжБЯпгаЧвжЛгавЛЬѕЃЛ
ЯрЧаЕФжБЯпгаЧвжЛгавЛЬѕЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌВЛЕШЪН
ЪБЃЌВЛЕШЪН![]() КуГЩСЂЃЌЧѓЪЕЪ§
КуГЩСЂЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНУцPACЁЭЦНУцABCЃЌ![]() ЪЧвдACЮЊаББпЕФЕШбќжБНЧШ§НЧаЮЃЌEЃЌFЃЌOЗжБ№ЮЊPAЃЌPBЃЌACЕФжаЕуЃЌ
ЪЧвдACЮЊаББпЕФЕШбќжБНЧШ§НЧаЮЃЌEЃЌFЃЌOЗжБ№ЮЊPAЃЌPBЃЌACЕФжаЕуЃЌ![]() .
.

ЃЈ1ЃЉЩшGЪЧOCЕФжаЕуЃЌжЄУїЃК![]() ЁЮЦНУц
ЁЮЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉжЄУїЃКдк![]() ФкДцдквЛЕуMЃЌЪЙFMЁЭЦНУцBOEЃЌЧѓЕуMЕНOAЃЌOBЕФОрРы.
ФкДцдквЛЕуMЃЌЪЙFMЁЭЦНУцBOEЃЌЧѓЕуMЕНOAЃЌOBЕФОрРы.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјЖЈЭждВ![]()
![]() ЃЌГЦдВаФдкдЕу
ЃЌГЦдВаФдкдЕу![]() ЃЌАыОЖЮЊ
ЃЌАыОЖЮЊ![]() ЕФдВЪЧЭждВ
ЕФдВЪЧЭждВ![]() ЕФЁАзМдВЁБ.ШєЭждВ
ЕФЁАзМдВЁБ.ШєЭждВ![]() ЕФвЛИіНЙЕуЮЊ
ЕФвЛИіНЙЕуЮЊ![]() ЃЌЦфЖЬжсЩЯЕФвЛИіЖЫЕуЕН
ЃЌЦфЖЬжсЩЯЕФвЛИіЖЫЕуЕН![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() .
.
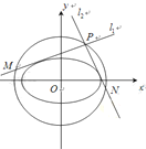
ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬКЭЦфЁАзМдВЁБЗНГЬЃЛ
ЕФЗНГЬКЭЦфЁАзМдВЁБЗНГЬЃЛ
ЃЈ2ЃЉЕу![]() ЪЧЭждВ
ЪЧЭждВ![]() ЕФЁАзМдВЁБЩЯЕФЖЏЕуЃЌЙ§Еу
ЕФЁАзМдВЁБЩЯЕФЖЏЕуЃЌЙ§Еу![]() зїЭждВЕФЧаЯп
зїЭждВЕФЧаЯп![]() НЛЁАзМдВЁБгкЕу
НЛЁАзМдВЁБгкЕу![]() .
.
ЂйЕБЕу![]() ЮЊЁАзМдВЁБгы
ЮЊЁАзМдВЁБгы![]() жсе§АыжсЕФНЛЕуЪБЃЌЧѓжБЯп
жсе§АыжсЕФНЛЕуЪБЃЌЧѓжБЯп![]() ЕФЗНГЬВЂжЄУї
ЕФЗНГЬВЂжЄУї![]() ЃЛ
ЃЛ
ЂкЧѓжЄЃКЯпЖЮ![]() ЕФГЄЮЊЖЈжЕ.
ЕФГЄЮЊЖЈжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкШЋУцПЙЛїаТЙкЗЮбзвпЧщетвЛЬиЪтЪБЦкЃЌЮвЪаНЬг§ОжЬсГіЁАЭЃПЮВЛЭЃбЇЁБЕФПкКХЃЌЙФРјбЇЩњЯпЩЯбЇЯА.ФГаЃЪ§бЇНЬЪІЮЊСЫЕїВщИпШ§бЇЩњЪ§бЇГЩМЈгыЯпЩЯбЇЯАЪБМфжЎМфЕФЯрЙиЙиЯЕЃЌЖдИпШ§ФъМЖЫцЛњбЁШЁ45УћбЇЩњНјааИњзйЮЪОэЃЌЦфжаУПжмЯпЩЯбЇЯАЪ§бЇЪБМфВЛЩйгк5аЁЪБЕФга19ШЫЃЌгрЯТЕФШЫжаЃЌдкМьВтПМЪджаЪ§бЇЦНОљГЩМЈВЛзу120ЗжЕФеМ![]() ЃЌЭГМЦГЩМЈКѓЕУЕНШчЯТ
ЃЌЭГМЦГЩМЈКѓЕУЕНШчЯТ![]() СаСЊБэЃК
СаСЊБэЃК
ЗжЪ§ВЛЩйгк120Зж | ЗжЪ§ВЛзу120Зж | КЯМЦ | |
ЯпЩЯбЇЯАЪБМфВЛЩйгк5аЁЪБ | 4 | 19 | |
ЯпЩЯбЇЯАЪБМфВЛзу5аЁЪБ | |||
КЯМЦ | 45 |
ЃЈ1ЃЉЧыЭъГЩЩЯУц![]() СаСЊБэЃЛВЂХаЖЯЪЧЗёга99%ЕФАбЮеШЯЮЊЁАИпШ§бЇЩњЕФЪ§бЇГЩМЈгыбЇЩњЯпЩЯбЇЯАЪБМфгаЙиЁБЃЛ
СаСЊБэЃЛВЂХаЖЯЪЧЗёга99%ЕФАбЮеШЯЮЊЁАИпШ§бЇЩњЕФЪ§бЇГЩМЈгыбЇЩњЯпЩЯбЇЯАЪБМфгаЙиЁБЃЛ
ЃЈ2ЃЉЂйАДееЗжВуГщбљЕФЗНЗЈЃЌдкЩЯЪібљБОжаДгЗжЪ§ВЛЩйгк120ЗжКЭЗжЪ§ВЛзу120ЗжЕФСНзщбЇЩњжаГщШЁ9УћбЇЩњЃЌЩшГщЕНВЛзу120ЗжЧвУПжмЯпЩЯбЇЯАЪБМфВЛзу5аЁЪБЕФШЫЪ§ЪЧ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЗжВМСаЃЈИХТЪгУзщКЯЪ§ЫуЪНБэЪОЃЉЃЛ
ЕФЗжВМСаЃЈИХТЪгУзщКЯЪ§ЫуЪНБэЪОЃЉЃЛ
ЂкШєНЋЦЕТЪЪгЮЊИХТЪЃЌДгШЋаЃИпШ§ИУДЮМьВтЪ§бЇГЩМЈВЛЩйгк120ЗжЕФбЇЩњжаЫцЛњГщШЁ20ШЫЃЌЧѓетаЉШЫжаУПжмЯпЩЯбЇЯАЪБМфВЛЩйгк5аЁЪБЕФШЫЪ§ЕФЦкЭћКЭЗНВю.
ЃЈЯТУцЕФСйНчжЕБэЙЉВЮПМЃЉ
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ЃЈВЮПМЙЋЪН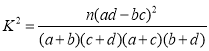 Цфжа
Цфжа![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЕФНЙОрЮЊ2ЃЌЧвГЄжсГЄЪЧЖЬжсГЄЕФ
ЕФНЙОрЮЊ2ЃЌЧвГЄжсГЄЪЧЖЬжсГЄЕФ![]() БЖ.
БЖ.
ЃЈ1ЃЉЧѓЭждВ![]() ЕФБъзМЗНГЬЃЛ
ЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉШєЙ§ЭждВ![]() зѓНЙЕу
зѓНЙЕу![]() ЕФжБЯп
ЕФжБЯп![]() НЛЭждВ
НЛЭждВ![]() гк
гк![]() СНЕуЃЌЕу
СНЕуЃЌЕу![]() дк
дк![]() жсЗЧИКАыжсЩЯЃЌЧвЕу
жсЗЧИКАыжсЩЯЃЌЧвЕу![]() ЕНзјБъдЕуЕФОрРыЮЊ2ЃЌЧѓ
ЕНзјБъдЕуЕФОрРыЮЊ2ЃЌЧѓ![]() ШЁЕУзюДѓжЕЪБ
ШЁЕУзюДѓжЕЪБ![]() ЕФУцЛ§.
ЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвдзјБъдЕуOЮЊМЋЕуЃЌxжсе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌЕу![]() ЃЌЃЈ
ЃЌЃЈ![]() ЃЉдкЧњЯпCЃК
ЃЉдкЧњЯпCЃК![]() ЩЯЃЌжБЯпlЙ§Еу
ЩЯЃЌжБЯпlЙ§Еу![]() Чвгы
Чвгы![]() ДЙжБЃЌДЙзуЮЊPЃЎ
ДЙжБЃЌДЙзуЮЊPЃЎ
ЃЈЂёЃЉЕБ![]() ЪБЃЌЧѓдкжБНЧзјБъЯЕЯТЕуPзјБъКЭlЕФЗНГЬЃЛ
ЪБЃЌЧѓдкжБНЧзјБъЯЕЯТЕуPзјБъКЭlЕФЗНГЬЃЛ
ЃЈЂђЃЉЕБMдкCЩЯдЫЖЏЧвPдкЯпЖЮ![]() ЩЯЪБЃЌЧѓЕуPдкМЋзјБъЯЕЯТЕФЙьМЃЗНГЬЃЎ
ЩЯЪБЃЌЧѓЕуPдкМЋзјБъЯЕЯТЕФЙьМЃЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com