
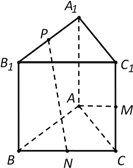
【题目】如图,直三棱柱ABC-A1B1C1中, AB=AC=AA1,AB⊥AC,M是CC1的中点,N是BC的中点,点P在线段A1B1上运动.
(Ⅰ)求证:PN⊥AM;
(Ⅱ)试确定点P的位置,使直线PN和平面ABC所成的角
最大.
科目:高中数学 来源: 题型:
【题目】某地上年度电价为0.8元,年用电量为1亿千瓦时.本年度计划将电价调至0.55元~0.75元之间,经测算,若电价调至![]() 元,则本年度新增用电量
元,则本年度新增用电量![]() (亿千瓦时)与
(亿千瓦时)与![]() 元成反比例.又当
元成反比例.又当![]() 时,
时,![]() .
.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)若每千瓦时电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年增加20%?[收益![]() 用电量
用电量![]() (实际电价-成本价)]
(实际电价-成本价)]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 过椭圆
过椭圆![]() :
: ![]() (
(![]() )的短轴端点,
)的短轴端点, ![]() ,
, ![]() 分别是圆
分别是圆![]() 与椭圆
与椭圆![]() 上任意两点,且线段
上任意两点,且线段![]() 长度的最大值为3.
长度的最大值为3.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 作圆
作圆![]() 的一条切线交椭圆
的一条切线交椭圆![]() 于
于![]() ,
, ![]() 两点,求
两点,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】口袋中装有2个白球和n(n≥2,n![]() N*)个红球.每次从袋中摸出2个球(每次摸球后把这2个球放回口袋中),若摸出的2个球颜色相同则为中奖,否则为不中奖.
N*)个红球.每次从袋中摸出2个球(每次摸球后把这2个球放回口袋中),若摸出的2个球颜色相同则为中奖,否则为不中奖.
(I)用含n的代数式表示1次摸球中奖的概率;
(Ⅱ)若n=3,求3次摸球中恰有1次中奖的概率;
(III)记3次摸球中恰有1次中奖的概率为f(p),当f(p)取得最大值时,求n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家用电器公司生产一新款热水器,首先每年需要固定投入 200万元,其次每生产1百台,需再投入0.9万元.假设该公司生产的该款热水器当年能全部售出,但每销售1百台需另付运输费0.1万元.根据以往的经验,年销售总额![]() (万元)关于年产量
(万元)关于年产量![]() (百台)的函数为
(百台)的函数为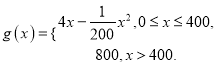 .
.
(1)将年利润![]() 表示为年产量
表示为年产量![]() 的函数;
的函数;
(2)求该公司生产的该款热水器的最大年利润及相应的年产量.
查看答案和解析>>
科目:高中数学 来源: 题型:
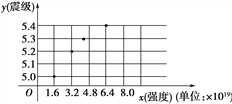
【题目】某地区发生里氏8.0级特大地震.地震专家对发生的余震进行了监测,记录的部分数据如下表:
强度(J) | 1.6×1019 | 3.2×1019 | 4.5×1019 | 6.4×1019 |
震级(里氏) | 5.0 | 5.2 | 5.3 | 5.4 |
注:地震强度是指地震时释放的能量.
地震强度(x)和震级(y)的模拟函数关系可以选用y=alg x+b(其中a,b为常数).利用散点图(如图)可知a的值等于________.(取lg 2=0.3进行计算)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com