3名志愿者在10月1号至10月5号期间参加社区服务工作.
(Ⅰ)若每名志愿者在这5天中任选一天参加社区服务工作,且各志愿者的选择互不影响,求3名志愿者恰好连续3天参加社区服务工作的概率;
(Ⅱ)若每名志愿者在这5天中任选两天参加社区服务工作,且各志愿者的选择互不影响,记ξ表示这3名志愿者在10月1号参加社区服务工作的人数,求随机变量ξ的分布列.
分析:(Ⅰ)由题意知3名志愿者每人任选一天参加社区服务,共有53种不同的结果,这些结果出现的可能性都相等.满足条件的事件是3名志愿者恰好连续3天参加社区服务工作共包括3A33不同的结果.根据概率公式做出概率.
(II)ξ表示这3名志愿者在10月1号参加社区服务工作的人数,随机变量ξ的可能取值为0,1,2,3,类似于第一问的做法,写出变量的分布列,或者不同可以先判断变量服从二项分布,利用二项分布的公式,得到要求的结果.
解答:解:(Ⅰ)3名志愿者每人任选一天参加社区服务,共有5
3种不同的结果,这些结果出现的可能性都相等.
设“3名志愿者恰好连续3天参加社区服务工作”为事件A则该事件共包括3A
33不同的结果.
所以
P(A)==.
即3名志愿者恰好连续3天参加社区服务工作的概率为
.
(Ⅱ)解法1:随机变量ξ的可能取值为0,1,2,3.
P(ξ=0)==,P(ξ=1)==,
P(ξ=2)==,P(ξ=3)==.
随机变量ξ的分布列为:
解法2:日参加社区服务的概率均为
P==.
则三名志愿者在10月1日参加社区服务的人数
ξ?B(3,).
P(ξ=i)=()i()3-i,i=0,1,2,3
∴分布列为:
点评:本题考查离散型随机变量的分布列,考查二项分布的应用,考查独立重复试验的概率公式,考查利用概率只是解决实际问题的能力,是一个综合题目.



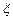 表示这3名志愿者在10月1号参加志愿者服务工作的人数,求随机变量
表示这3名志愿者在10月1号参加志愿者服务工作的人数,求随机变量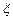 的数学期望.
的数学期望.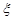 表示这3名志愿者在10月1号参加志愿者服务工作的人数,求随机变量
表示这3名志愿者在10月1号参加志愿者服务工作的人数,求随机变量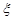 的数学期望.
的数学期望.