
【题目】直四棱柱ABCD﹣A1B1C1D1中,底面ABCD为菱形,且∠BAD=60°,A1A=AB,E为BB1延长线上的一点,D1E⊥面D1AC.设AB=2. 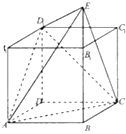
(1)求二面角E﹣AC﹣D1的大小;
(2)在D1E上是否存在一点P,使A1P∥面EAC?若存在,求D1P:PE的值;不存在,说明理由.
【答案】
(1)解:设AC与BD交于O,
如图以O为原点,OA,OB,为x轴,y轴,过O作面ABCD的垂线为z轴,建立空间直角坐标系,
则A( ![]() ,0,0),B(0,1,0),C(﹣
,0,0),B(0,1,0),C(﹣ ![]() ,0,0),D(0,﹣1,0),D1(0,﹣1,2),
,0,0),D(0,﹣1,0),D1(0,﹣1,2),
设E(0,1,2+h),
则 ![]() =(0,2,h),
=(0,2,h), ![]() =(2
=(2 ![]() ,0,0),
,0,0), ![]() =(
=( ![]() ),
),
∵D1E⊥平面D1AC,∴D1E⊥AC,D1E⊥D1A,
∴2﹣2h=0,∴h=1,即E(0,1,3),
∴ ![]() =(0,2,1),
=(0,2,1), ![]() =(﹣
=(﹣ ![]() ,1,3),
,1,3),
设平面EAC的法向量为 ![]() =(x,y,z),
=(x,y,z),
则由 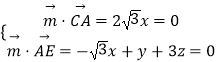 ,令z=﹣1,得
,令z=﹣1,得 ![]() =(0,3,﹣1),
=(0,3,﹣1),
∵D1E⊥面D1AC,∴平面D1AC的法向量为 ![]() =(0,2,1),
=(0,2,1),
∴cos< ![]() >=
>= 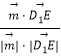 =
= ![]() =
= ![]() ,
,
∴二面角E﹣AC﹣D1的大小为45°.

(2)解:设 ![]() =
= ![]() =λ(
=λ( ![]() ),
),
得 ![]() =
= ![]() =(0,
=(0, ![]() ,
, ![]() ),
),
∴ ![]() =
= ![]() +
+ ![]() =(﹣
=(﹣ ![]() ,﹣1,0)+(0,
,﹣1,0)+(0, ![]() ,
, ![]() )=(﹣
)=(﹣ ![]() ,
, ![]() ,
, ![]() ),
),
∵A1P∥面EAC,∴ ![]() ⊥
⊥ ![]() ,
,
∴﹣ ![]() =0,
=0,
解得 ![]() ,
,
∴存在点P使A1P∥面EAC,此时D1P:PE=2:3.
【解析】(1)设AC与BD交于O,以O为原点,OA,OB,为x轴,y轴,过O作面ABCD的垂线为z轴,建立空间直角坐标系,利用向量法能求出二面角E﹣AC﹣D1的大小.(2)设 ![]() =
= ![]() =λ(
=λ( ![]() ),得
),得 ![]() =(0,
=(0, ![]() ,
, ![]() ),
), ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,
, ![]() ),由此能求出存在点P使A1P∥面EAC,此时D1P:PE=2:3.
),由此能求出存在点P使A1P∥面EAC,此时D1P:PE=2:3.
【考点精析】关于本题考查的直线与平面平行的判定,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行才能得出正确答案.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,AA1=AD=1,E为CD的中点. 
(1)求证:B1E⊥AD1
(2)若二面角A﹣B1E﹣A1的大小为30°,求AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=SB,点M是SD的中点,AN⊥SC,且交SC于点N. 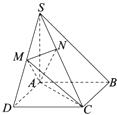
(1)求证:SC⊥平面AMN;
(2)求二面角D﹣AC﹣M的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】与圆(x+1)2+y2=1和圆(x﹣5)2+y2=9都相切的圆的圆心轨迹是( )
A.椭圆和双曲线
B.两条双曲线
C.双曲线的两支
D.双曲线的一支
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x),(x∈R)上任一点(x0 , y0)的切线方程为y﹣y0=(x0﹣2)(x02﹣1)(x﹣x0),那么函数f(x)的单调递减区间是( )
A.[﹣1,+∞)
B.(﹣∞,2]
C.(﹣∞,﹣1)和(1,2)
D.[2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们把形如 ![]() 的函数称为幂指函数,幂指函数在求导时,可以利用对法数:在函数解析式两边求对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对法数:在函数解析式两边求对数得 ![]() ,两边对x求导数,得
,两边对x求导数,得 ![]() ,于是
,于是 ![]() ,运用此方法可以求得函数
,运用此方法可以求得函数 ![]() 在(1,1)处的切线方程是 .
在(1,1)处的切线方程是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩形ABCD中,AB=2,AD=1,M为CD的中点.如图将△ADM沿AM折起,使得平面ADM⊥平面ABCM.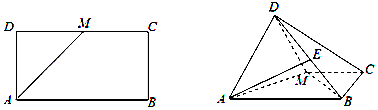
(Ⅰ)求证:BM⊥平面ADM;
(Ⅱ)若点E是线段DB上的中点,求三棱锥E﹣ABM的体积V1与四棱锥D﹣ABCM的体积V2之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图正方体ABCD﹣A1B1C1D1 , M,N分别为A1D1和AA1的中点,则下列说法中正确的个数为( ) 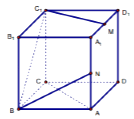
①C1M∥AC;
②BD1⊥AC;
③BC1与AC的所成角为60°;
④B1A1、C1M、BN三条直线交于一点.
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com