
【题目】设![]() 是
是![]() 在点
在点![]() 处的切线.
处的切线.
(![]() )求
)求![]() 的解析式.
的解析式.
(![]() )求证:
)求证: ![]() .
.
(![]() )设
)设![]() ,其中
,其中![]() .若
.若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】试题分析:(1)第(1)问,利用导数的几何意义求切线方程即得y=f(x). (2)第(2)问,转化成证明![]() ,即证明[f(x)-g(x)]的最大值小于等于零.(3),第(3)问,对a分类讨论,求函数
,即证明[f(x)-g(x)]的最大值小于等于零.(3),第(3)问,对a分类讨论,求函数![]() 的单调区间和最小值,找到a的范围.
的单调区间和最小值,找到a的范围.
试题解析:
(![]() )由
)由![]() 得
得![]() ,∴
,∴![]() ,
, ![]() ,
,
∴![]() 在点
在点![]() 处的切线方程为:
处的切线方程为: ![]() ,即
,即![]() ,
,
∴![]() 的解析式为:
的解析式为: ![]() .
.
(![]() )令
)令![]() ,则
,则![]() ,
,
由![]() 得
得![]() ,由
,由![]() ,得
,得![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]() ,即
,即![]() ,∴
,∴![]() .
.
(![]() )
)![]() 的定义域是
的定义域是![]() ,且
,且![]() .
.
①![]() 时,由(
时,由(![]() )得:
)得: ![]() ,
,
∴![]() ,
,
∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() 恒成立,符合题意;
恒成立,符合题意;
②![]() 时,由
时,由![]() ,且
,且![]() 的导数
的导数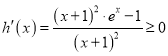 ,
,
∴![]() 在区间
在区间![]() 上单调递增,
上单调递增,
∵![]() ,
, ![]() ,
,
∴存在![]() ,使得
,使得![]() ,
,
∴![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,∴
上单调递增,∴![]() ,
,
此时, ![]() 不可能恒成立,不符合题意,
不可能恒成立,不符合题意,
综上所述, ![]() 的取值范围是
的取值范围是![]() .
.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=2,直线.l:y=kx-2.
(1)若直线l与圆O相切,求k的值;
(2)若直线l与圆O交于不同的两点A,B,当∠AOB为锐角时,求k的取值范围;
(3)若![]() ,P是直线l上的动点,过P作圆O的两条切线PC,PD,切点为C,D,探究:直线CD是否过定点.
,P是直线l上的动点,过P作圆O的两条切线PC,PD,切点为C,D,探究:直线CD是否过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班同学利用国庆节进行社会实践,对![]() 岁的人群随机抽取
岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 |
| 120 | 0.6 |
第二组 |
| 195 |
|
第三组 |
| 100 | 0.5 |
第四组 |
|
| 0.4 |
第五组 |
| 30 | 0.3 |
第六组 |
| 15 | 0.3 |
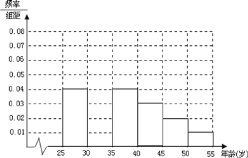
(1)补全频率分布直方图并求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)从![]() 岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动,如何抽取?
岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动,如何抽取?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图象如图所示,且相邻的两个最值点的距离为
的部分图象如图所示,且相邻的两个最值点的距离为![]() .
.

(1)求函数![]() 的解析式;
的解析式;
(2)若将函数![]() 的图象向左平移1个单位长度后得到函数
的图象向左平移1个单位长度后得到函数![]() 的图象,关于
的图象,关于![]() 的不等式
的不等式![]() 在
在![]() 上有解,求
上有解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆的中心在原点,焦点在![]() 轴上,长轴长是短轴长的2倍且经过点
轴上,长轴长是短轴长的2倍且经过点![]() ,平行于
,平行于![]() 的直线
的直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,直线
,直线![]() 交椭圆于
交椭圆于![]() 两个不同点.
两个不同点.

(1)求椭圆的方程;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合P={x|a+1≤x≤2a+1},Q={x|x2-3x≤10}.
(1)若a=3,求(RP)∩Q;
(2)若P∪Q=Q,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂要建造一个长方形无盖蓄水池,其容积为![]() 立方米,深为
立方米,深为![]() .如果池底每平方米的造价为
.如果池底每平方米的造价为![]() 元,池壁每平方米的造价为
元,池壁每平方米的造价为![]() 元,那么怎样设计水池能使总造价最低(设蓄水池池底的相邻两边边长分别为
元,那么怎样设计水池能使总造价最低(设蓄水池池底的相邻两边边长分别为![]() ,
,![]() )?最低总造价是多少?
)?最低总造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.

(Ⅰ)证明 PA//平面EDB;
(Ⅱ)证明PB⊥平面EFD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com