
【题目】某工厂生产某款机器零件,因为要求精度比较高,所以需要对生产的一大批零件进行质量检测.首先由专家根据各种系数制定了质量指标值,从生产的大批零件中选取100件作为样本进行评估,根据评估结果作出如图所示的频率分布直方图.
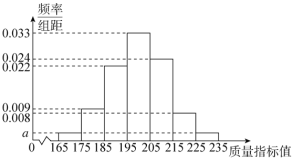
(1)(ⅰ)根据直方图求![]() 及这100个零件的样本平均数
及这100个零件的样本平均数![]() (同一组数据用该组数据区间的中点值表示);
(同一组数据用该组数据区间的中点值表示);
(ⅱ)以样本估计总体,经过专家研究,零件的质量指标值![]() ,试估计10000件零件质量指标值在
,试估计10000件零件质量指标值在![]() 内的件数;
内的件数;
(2)设每个零件利润为![]() 元,质量指标值为
元,质量指标值为![]() ,利润
,利润![]() 与质量指标值
与质量指标值![]() 之间满足函数关系
之间满足函数关系![]() .假设同组中的每个数据用该组区间的中点值代替,试估算该批零件的平均利润.(结果四舍五入,保留整数)
.假设同组中的每个数据用该组区间的中点值代替,试估算该批零件的平均利润.(结果四舍五入,保留整数)
参考数据:![]() ,则
,则![]() ,
,![]() ,
,![]()
科目:高中数学 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭人均纯收入y(单位:千元)的数据如下表:
年 份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
![]() =
= ,
,![]() =
=![]() -
-![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】政府为了稳定房价,决定建造批保障房供给社会,计划用![]() 万的价格购得一块建房用地,在该土地上建
万的价格购得一块建房用地,在该土地上建![]() 幢楼房供使用,每幢楼的楼层数相同且每层建
幢楼房供使用,每幢楼的楼层数相同且每层建![]() 套每套
套每套![]() 平方米,经测算第
平方米,经测算第![]() 层每平方米的建筑造价
层每平方米的建筑造价![]() (元)与
(元)与![]() 满足关系式
满足关系式![]() (其中
(其中![]() 为整数且被
为整数且被![]() 整除) ,根据某工程师的个人测算可知,该小区只有每幢建
整除) ,根据某工程师的个人测算可知,该小区只有每幢建![]() 层时每平方米平均综合费用才达到最低,其中每平方米
层时每平方米平均综合费用才达到最低,其中每平方米![]() .
.
(1)求![]() 的值;
的值;
(2)为使该小区平均每平方米的平均综合费用控制在![]() 元以内,每幢至少建几层?至多造几层?
元以内,每幢至少建几层?至多造几层?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱![]() 中,底面
中,底面![]() 是以
是以![]() 为斜边的等腰直角三角形,侧面
为斜边的等腰直角三角形,侧面![]() 是菱形且与底面
是菱形且与底面![]() 垂直,
垂直,![]() ,点
,点![]() 是
是![]() 中点,点
中点,点![]() 是
是![]() 上靠近
上靠近![]() 点的三等分点.
点的三等分点.
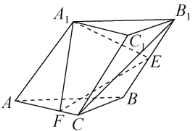
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若函数![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,求实数
上递增,求实数![]() 的值.
的值.
(2)若函数![]() 在定义域上不单调,求实数
在定义域上不单调,求实数![]() 的取值范围.
的取值范围.
(3)若方程![]() 有两个不等实数根
有两个不等实数根![]() ,求实数
,求实数![]() 的取值范围,并证明
的取值范围,并证明![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《汉字听写大会》不断创收视新高,为了避免“书写危机”,弘扬传统文化,某市大约10万名市民进行了汉字听写测试.现从某社区居民中随机抽取50名市民的听写测试情况,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第1组![]() ,第2组
,第2组![]() ,…,第6组
,…,第6组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.

(1)若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第2组或第6组的概率;
(2)试估计该市市民正确书写汉字的个数的众数与中位数;
(3)已知第4组市民中有3名男性,组织方要从第4组中随机抽取2名市同组成弘扬传统文化宣传队,求至少有1名女性市民的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,A(﹣2,0),B(2,0),P为不在x轴上的动点,直线PA,PB的斜率满足kPAkPB![]() .
.
(1)求动点P的轨迹Γ的方程;
(2)若M,N是轨迹Γ上两点,kMN=1,求△OMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足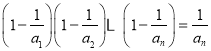 ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)已知数列![]() 的通项公式为
的通项公式为![]() ,若对于一切
,若对于一切![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)设![]() ,是否存在正整数
,是否存在正整数![]() ,使得数列
,使得数列![]() 中存在某项
中存在某项![]() 满足
满足![]() 成等差数列?若存在,求出符合题意的
成等差数列?若存在,求出符合题意的![]() 的集合;若不存在,请说明理由.
的集合;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com