
分析 (1)通过讨论x的范围,求出不等式的解集即可;(2)问题转化为a≤|x-2|+|x|,根据绝对值的意义,求出a的范围即可.
解答 解:(1)f(x)≥0,即|x-2|-|2x|+3≥0,
x≤0时,2-x+2x+3≥0,解得:0≥x≥-5,
0<x<2时,2-x-2x+3≥0,解得:0<x≤$\frac{5}{3}$,
x≥2时,x-2-2x+3≥0,解得:x≤1,无解,
综上,不等式的解集是[0,$\frac{5}{3}$];
(2))若对任意实数x,f(x)≥a-3|x|,
即对任意实数x,|x-2|-|2x|+3≥a-3|x|,
即a≤|x-2|+|x|,
而|x-2|+|x|≥|x-2-x|=2,
故a≤2.
点评 本题考查了绝对值的性质,考查分类讨论思想,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<1} | B. | {x|x>1} | C. | {x|x<-1或x>1} | D. | {x|x<-1或0<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2-$\sqrt{3}$ | B. | $\sqrt{3}$-1 | C. | $\frac{2-\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
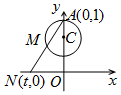 如图,周长为1的圆的圆心C在y轴上,一动点M从圆上的点A(0,1)开始按逆时针方向绕圆运动一周,记走过的弧长为x,直线AM与x轴交于点N(t,0),则函数t=f(x)的图象大致为( )
如图,周长为1的圆的圆心C在y轴上,一动点M从圆上的点A(0,1)开始按逆时针方向绕圆运动一周,记走过的弧长为x,直线AM与x轴交于点N(t,0),则函数t=f(x)的图象大致为( )| A. | 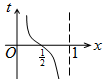 | B. | 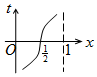 | C. | 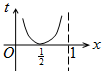 | D. | 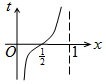 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com