
【题目】设命题p:方程x2+(2m-4)x+m=0有两个不等的实数根:命题q:x∈[2,3],不等式x2-4x+13≥m2恒成立.
(1)若命题p为真命题,则实数m的取值范围;
(2)若命题p∨q为真命题,命题p∧q为假命题,求实数m的取值范围.
【答案】(1)m>4或m<1;(2)m<-3或1≤m≤3或m>4
【解析】
(1)根据一元二次方程根与判别式△的关系求出m的范围即可.
(2)求出命题p,q为真命题的等价条件,结合复合命题真假关系进行求解即可.
(1)若命题p为真命题,则判别式△=(2m-4)2-4m=4(m-1)(m-4)>0,
解得m>4或m<1.
(2)若命题q为真命题,则(x-2)2≥m2-9在[2,3]恒成立.
∵当x=2时,(x-2)2取得最小值0,
则0≥m2-9,即m2≤3,解得![]() .
.
“若命题p∨q为真命题,命题p∧q为假命题,所以命题p,q中一真一假,
当p真且q假时,![]() ,得m<-3或m>4,
,得m<-3或m>4,
当p假且q真时,![]() ,解得1≤m≤3.
,解得1≤m≤3.
综上所述:m<-3或1≤m≤3或m>4.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】给出下列命题:
(1)函数![]() 的图象关于点
的图象关于点![]() 对称;
对称;
(2)函数![]() 在区间
在区间![]() 内是增函数;
内是增函数;
(3)函数![]() 是偶函数;
是偶函数;
(4)存在实数![]() ,使
,使![]() ;
;
(5)如果函数![]() 的图象关于点
的图象关于点![]() 中心对称,那么
中心对称,那么![]() 的最小值为
的最小值为![]() .
.
其中正确的命题的序号是___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站退出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组
.现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
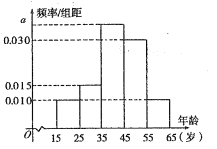
(1)求出![]() 的值;
的值;
(2)求这200人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(3)现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求这2组恰好抽到2人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,E是PC的中点,底面ABCD为矩形,AB=4,AD=2,PA=PD,且平面PAD⊥平面ABCD,平面ABE与棱PD交于点F.

(1)求证:EF∥平面PAB;
(2)若PB与平面ABCD所成角的正弦值为![]() ,求二面角P-AE-B的余弦值.
,求二面角P-AE-B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体![]() ,
, ![]() ,
,![]()
![]() ,且
,且![]() 两两垂直.给出下列四个命题:
两两垂直.给出下列四个命题:

①三棱锥![]() 的体积为定值;
的体积为定值;
②经过![]() 四点的球的直径为
四点的球的直径为![]() ;
;
③直线![]() ∥平面
∥平面![]() ;
;
④直线![]() 所成的角为
所成的角为![]() ;
;
其中真命题的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+![]() .
.
(1)若关于x的不等式f(3x)≤m3x+2在[-2,2]上恒成立.求实数m的取值范围;
(2)若函数g(x)=f(|2x-1|)![]() -3t-2有四个不同的零点,求实数t的取值范围.
-3t-2有四个不同的零点,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】试用恰当的方法表示下列集合.
(1)使函数![]() 有意义的x的集合;
有意义的x的集合;
(2)不大于12的非负偶数;
(3)满足不等式![]() 的解集;
的解集;
(4)由大于10小于20的所有整数组成的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了加强中学生实践、创新和团队建设能力的培养,促进教育教学改革,市教育局举办了全市中学生创新知识竞赛,某中学举行了选拔赛,共有150名学生参加,为了了解成绩情况,从中抽取50名学生的成绩(得分均为整数,满分为100分)进行统计,请你根据尚未完成的频率分布表,解答下列问题:
(1)完成频率分布表(直接写出结果);
(2)若成绩在90.5分以上的学生获一等奖,试估计全校获一等奖的人数,现在从全校所有获一等奖的同学中随机抽取2名同学代表学校参加竞赛,某班共有2名同学荣获一等奖,求该班同学恰有1人参加竞赛的概率.
分组 | 频数 | 频率 | |
第1组 | [60.5,70.5) | 0.26 | |
第2组 | [70.5,80.5) | 17 | |
第3组 | [80.5,90.5) | 18 | 0.36 |
第4组 | [90.5,100.5] | ||
合计 | 50 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的十八大以来,我国精准扶贫已经实施了六年,我国贫困人口从2012年的9899万人,减少到2018年的1660万人,2019年将努力实现减少贫困人口1000万人以上的目标,力争2020年在现行标准下,农村贫困人口全部脱贫,贫困县全部脱贫摘帽.某市为深入分析该市当前扶贫领域存在的突出问题,市扶贫办近三年来,每半年对贫困户(用![]() 表示,单位:万户)进行取样,统计结果如图所示,从2016年6月底到2019年6月底的共进行了七次统计,统计时间用序号
表示,单位:万户)进行取样,统计结果如图所示,从2016年6月底到2019年6月底的共进行了七次统计,统计时间用序号![]() 表示,例如:2016年12月底(时间序号为2)贫困户为5.2万户.
表示,例如:2016年12月底(时间序号为2)贫困户为5.2万户.
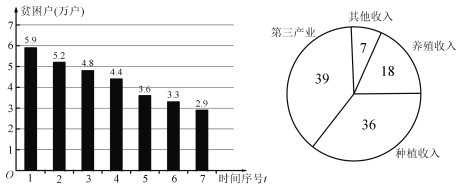
(1)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测到2020年12月底,该市能否实现贫困户全部脱贫;
,并预测到2020年12月底,该市能否实现贫困户全部脱贫;
(2)为尽快打赢脱贫攻坚战,该市扶贫办在2019年6月底时,对全市贫困户随机抽取了100户贫困户,对每个家庭最主要经济收入来源进行抽样调查,统计结果如图.并决定据此选派一批农业技术人员对全市所有贫困户中,家庭最主要经济收入来源为养殖收入和种植收入的贫困户进行对口帮扶,每一名农业技术人员对口帮扶贫困户90户,则该市应分别安排多少农业技术人员对家庭最主要经济收入来源为养殖收入和种植收入的贫困户进行对口帮扶?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
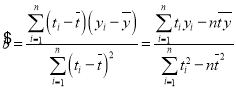 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com