
 在海岸A处,发现北偏东45°方向,距A处(
在海岸A处,发现北偏东45°方向,距A处(| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 6 |
| AC |
| BC |
| 2 | ||
|
| ||
| 2 |
| ||
| 2 |
| BD•sin∠CBD |
| CD |
| 10t•sin120° | ||
10
|
| 1 |
| 2 |


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 在海岸A处,发现北偏东45°方向,距离A为(
在海岸A处,发现北偏东45°方向,距离A为(| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 在海岸A处,发现北偏东45°方向,距离A(
在海岸A处,发现北偏东45°方向,距离A(| 3 |
| 3 |
| ||||
| 4 |
| ||||
| 4 |
查看答案和解析>>
科目:高中数学 来源:2015届湖南省高一4月段考数学试卷(解析版) 题型:解答题
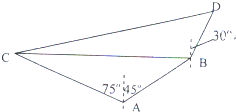
在海岸A处,发现北偏东45°方向距A为 -1海里的B处有一艘走私船,在A处北偏西75°的方向,距A为2海里的C处的缉私船奉命以10
-1海里的B处有一艘走私船,在A处北偏西75°的方向,距A为2海里的C处的缉私船奉命以10 海里/小时的速度追截走私船.此时走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船沿着什么方向能最快追上走私船?并求出所需要的时间.(注:
海里/小时的速度追截走私船.此时走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜,问缉私船沿着什么方向能最快追上走私船?并求出所需要的时间.(注: ≈2.449)
≈2.449)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com