
【题目】函数![]() 的图象关于直线
的图象关于直线![]() 对称,它的最小正周期是
对称,它的最小正周期是![]() ,则下列说法正确的是______.(填序号)
,则下列说法正确的是______.(填序号)
①![]() 的图象过点
的图象过点![]()
②![]() 在
在![]() 上是减函数
上是减函数
③![]() 的一个对称中心是
的一个对称中心是![]()
④将![]() 的图象向右平移
的图象向右平移![]() 个单位长度得到函数
个单位长度得到函数![]() 的图象
的图象
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() 、
、![]() ,并且直线
,并且直线![]() 平分圆
平分圆![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)若过点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 有两个不同的交点
有两个不同的交点![]() 、
、![]() .
.
(i)求实数![]() 的取值范围;
的取值范围;
(ii)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现要完成下列三项抽样调查:①从![]() 罐奶粉中抽取
罐奶粉中抽取![]() 罐进行食品安全卫生检查;②高二年级有
罐进行食品安全卫生检查;②高二年级有![]() 名学生,为调查学生的学习情况抽取一个容量为
名学生,为调查学生的学习情况抽取一个容量为![]() 的样本;③从某社区
的样本;③从某社区![]() 户高收入家庭,
户高收入家庭,![]() 户中等收入家庭,
户中等收入家庭,![]() 户低收入家庭中选出
户低收入家庭中选出![]() 户进行消费水平调查.以下各调查方法较为合理的是( )
户进行消费水平调查.以下各调查方法较为合理的是( )
A.①系统抽样,②简单随机抽样,③分层抽样
B.①简单随机抽样,②分层抽样,③系统抽样
C.①分层抽样,②系统抽样,③简单随机抽样
D.①简单随机抽样,②系统抽样,③分层抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() ,点
,点![]() .以点
.以点![]() 为中心,顺时针旋转矩形
为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]() .
.

(1)如图①,当点![]() 落在
落在![]() 边上时,求点
边上时,求点![]() 的坐标;
的坐标;
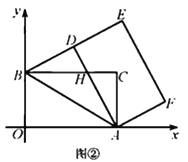
(2)如图②,当点![]() 落在线段
落在线段![]() 上时,
上时,![]() 与
与![]() 交于点
交于点![]() .
.
①求证![]() ;②求点
;②求点![]() 的坐标.
的坐标.
(3)记![]() 为矩形
为矩形![]() 对角线的交点,
对角线的交点,![]() 为
为![]() 的面积,求
的面积,求![]() 的取值范围(直接写出结果即可).
的取值范围(直接写出结果即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com