
 ;
; ;
;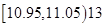 ;
; ;
; ;
; ;
; ;
;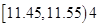 ;
; ;
; 范围内的可能性是百分之几?
范围内的可能性是百分之几? 范围内的频率为:
范围内的频率为: ,即数据落在
,即数据落在 范围内的可能性是75%。
范围内的可能性是75%。 ,则:
,则: 即得到。
即得到。| 分组 | 频数 | 频率 | 累积频率 |
| [10.75,10.85) | 3 | 0.03 | 0.03 |
| [10.85,10.95) | 9 | 0.09 | 0.12 |
| [10.95,11.05) | 13 | 0.13 | 0.25 |
| [11.05,11.15) | 16 | 0.16 | 0.41 |
| [11.15,11.25) | 26 | 0.26 | 0.67 |
| [11.25,11.35) | 20 | 0.20 | 0.87 |
| [11.35,11.45) | 7 | 0.07 | 0.94 |
| [11.45,11.55) | 4 | 0.04 | 0.98 |
| [11.55,11.65) | 2 | 0.02 | 1.00 |
| 合计 | 100 | 1.00 | |
 6分
6分 范围内的频率为:
范围内的频率为: ,即数据落在
,即数据落在 范围内的可能性是75%。 10分
范围内的可能性是75%。 10分 ,则:
,则: ,
, ,从而估计数据小于11.20的可能性是54%。 14分
,从而估计数据小于11.20的可能性是54%。 14分

科目:高中数学 来源:不详 题型:解答题
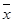 ,将10场比赛得分
,将10场比赛得分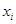 依次输入如图所示的程序框图进行运算,问输出的
依次输入如图所示的程序框图进行运算,问输出的 大小为多少?并说明
大小为多少?并说明 的统计学意义;
的统计学意义;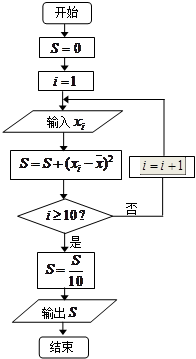
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 学生 | 1号 | 2号 | 3号 | 4号 | 5号 |
| 甲班 | 6 | 7 | 7 | 8 | 7 |
| 乙班 | 6 | 7 | 6 | 7 | 9 |
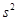 =
= 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段 ,
, …
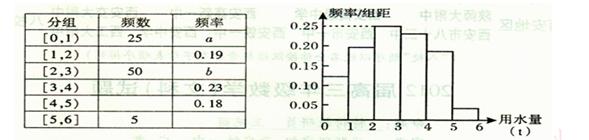
… 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图; 名学生中随机抽取
名学生中随机抽取 人,抽到的学生成绩在
人,抽到的学生成绩在 记
记 分,在
分,在 记
记 分,
分, 记
记 分,用
分,用 表示抽取结束后的总记分,求
表示抽取结束后的总记分,求 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 等待时间(分钟) | 频数 | 频率 |
| [0,3) | | 0.2 |
| [3,6) | | 0.4 |
| [6,9) | 5 | x |
| [9,12) | 2 | y |
| [12,15) | 1 | 0.05 |
| 合计 | z | 1 |
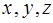 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.81.2,4.4 | B.78.8,4.4 | C.81.2,84.4 | D.78.8,75.6 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 辆汽车通过某一段公路时的时速有如下关系:
辆汽车通过某一段公路时的时速有如下关系:| 时速区间 | [40,50) | [50,60) | [60,70) | [70,80) |
| 辆数 | 10 | 30 | 40 | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com