
【题目】小王投资1万元2万元、3万元获得的收益分别是4万元、9万元、16万元为了预测投资资金x(万元)与收益y万元)之间的关系,小王选择了甲模型![]() 和乙模型
和乙模型![]() .
.
(1)根据小王选择的甲、乙两个模型,求实数a,b,c,p,q,r的值
(2)若小王投资4万元,获得收益是25.2万元,请问选择哪个模型较好?
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,如果![]() 与
与![]() 都是整数,就称点
都是整数,就称点![]() 为整点,下列命题中正确的是_____________(写出所有正确命题的编号)
为整点,下列命题中正确的是_____________(写出所有正确命题的编号)
①存在这样的直线,既不与坐标轴平行又不经过任何整点
②如果![]() 与
与![]() 都是无理数,则直线
都是无理数,则直线![]() 不经过任何整点
不经过任何整点
③直线![]() 经过无穷多个整点,当且仅当
经过无穷多个整点,当且仅当![]() 经过两个不同的整点
经过两个不同的整点
④直线![]() 经过无穷多个整点的充分必要条件是:
经过无穷多个整点的充分必要条件是:![]() 与
与![]() 都是有理数
都是有理数
⑤存在恰经过一个整点的直线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() ,
,![]() 为两条异面直线,
为两条异面直线,![]() ,
,![]() 为两个平面,
为两个平面,![]() ,
,![]() ,
,![]() ,则下列结论中错误的序号是______.
,则下列结论中错误的序号是______.
①![]() 至少与
至少与![]() ,
,![]() 中一条相交; ②
中一条相交; ②![]() 至多与
至多与![]() ,
,![]() 中一条相交;
中一条相交;
③![]() 至少与
至少与![]() ,
,![]() 中一条平行; ④
中一条平行; ④![]() 必与
必与![]() ,
,![]() 中一条相交,与另一条平行.
中一条相交,与另一条平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
B.对于命题![]() :
:![]() ,使得
,使得![]() ,则
,则![]() :
:![]() 均有
均有![]()
C.若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题
均为假命题
D.命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥S—ABCD中,∠SDA=2∠SAD=90°,∠BAD+∠ADC=180°,AB=![]() CD,点F是线段
CD,点F是线段
SA上靠近点A的一个三等分点,AC与BD相交于E.

(1)在线段SB上作出点G,使得平面EFG∥平面SCD,请指明点G的具体位置,并用阴影部分表示平面EFG,不必说明平面EFG∥平面SCD的理由;
(2)若SA=SB=2,AB=AD=BD=![]() ,求点F到平面SCD的距离.
,求点F到平面SCD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲乙两组学生,分别参加某项体能测试,所得成绩的茎叶图如图.规定测试成绩大于等于90分为优秀,80至89分为良好,60至79分为合格,60分以下为不合格.
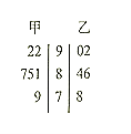
(1)现从甲组数据中抽取一名学生的成绩,有放回地抽取6次,记抽到优秀成绩的次数为X,求![]() ;
;
(2)从甲、乙两组学生中任取3名学生,记抽中成绩优秀的学生数为Y,求Y的概率分布与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]()
![]()
![]() ,若
,若![]() ,且
,且![]() 的图象相邻的对称轴间的距离不小于
的图象相邻的对称轴间的距离不小于![]() .
.
(1)求![]() 的取值范围.
的取值范围.
(2)若当![]() 取最大值时,
取最大值时, ![]() ,且在
,且在![]() 中,
中, ![]() 分别是角
分别是角![]() 的对边,其面积
的对边,其面积![]() ,求
,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com