
分析 根据正态分布的概率性质求出a的值,再化(x+a)2(ax-$\frac{1}{\sqrt{x}}$)5=(x2+6x+9)${(3x-\frac{1}{\sqrt{x}})}^{5}$;利用${(3x-\frac{1}{\sqrt{x}})}^{5}$展开式的通项公式求出含x2的系数,即可求出对应项的系数.
解答 解:随机变量X~N(2,32),均值是2,
且P(X≤1)=P(X≥a),
∴a=3;
∴(x+a)2(ax-$\frac{1}{\sqrt{x}}$)5=(x+3)2(3x-$\frac{1}{\sqrt{x}}$)5=(x2+6x+9)${(3x-\frac{1}{\sqrt{x}})}^{5}$;
又${(3x-\frac{1}{\sqrt{x}})}^{5}$展开式的通项公式为
Tr+1=${C}_{5}^{r}$•(3x)5-r•${(-\frac{1}{\sqrt{x}})}^{r}$=(-1)r•35-r•${C}_{5}^{r}$•${x}^{5-\frac{3r}{2}}$,
令5-$\frac{3r}{2}$=1,解得r=$\frac{8}{3}$,不合题意,舍去;
令5-$\frac{3r}{2}$=2,解得r=2,对应x2的系数为(-1)2•23•${C}_{5}^{2}$=270;
令5-$\frac{3r}{2}$=3,解得r=$\frac{4}{3}$,不合题意,舍去;
∴展开式中x3项的系数是6×270=1620.
故答案为:1620.
点评 本题考查了正态分布曲线的特点及其几何意义,也考查二项式系数的性质与应用问题,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$ | B. | 3 $\overrightarrow{AB}$ | C. | $\overrightarrow{BA}$ | D. | $\overrightarrow{CA}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,图中圆弧所在圆的圆心为点C,半径为$\frac{1}{2}$,且点P在图中阴影部分(包括边界)运动.若$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{BC}$,其中x,y∈R,则4x-y的取值范围是( )
如图,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,图中圆弧所在圆的圆心为点C,半径为$\frac{1}{2}$,且点P在图中阴影部分(包括边界)运动.若$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{BC}$,其中x,y∈R,则4x-y的取值范围是( )| A. | $[2,\;\;3+\frac{{3\sqrt{2}}}{4}]$ | B. | $[2,\;\;3+\frac{{\sqrt{5}}}{2}]$ | ||
| C. | $[3-\;\;\frac{{\sqrt{2}}}{4},\;\;3+\frac{{\sqrt{5}}}{2}]$ | D. | $[3-\;\;\frac{{\sqrt{17}}}{2},\;\;3+\;\frac{{\sqrt{17}}}{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 空气质量指数(μg/m3) | 0-50 | 51-100 | 101-150 | 151-200 | 201-250 |
| 空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 20 | 40 | m | 10 | 5 |
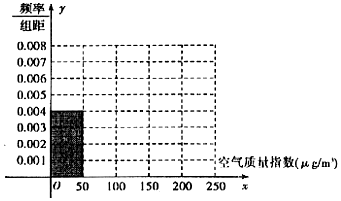
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高二理下学期期末考试数学试卷(解析版) 题型:填空题
先后掷骰子(骰子的六个面上分别标有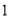 、
、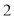 、
、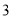 、
、 、
、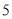 、
、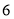 个点)两次,落在水平桌面后,记正面朝上的点数分别为
个点)两次,落在水平桌面后,记正面朝上的点数分别为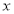 ,
,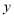 ,设事件
,设事件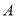 为“
为“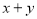 为偶数”, 事件
为偶数”, 事件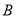 为 “
为 “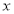 ,
,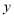 中有偶数且
中有偶数且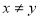 ”,则概率
”,则概率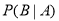 等于_________.
等于_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com