
【题目】如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
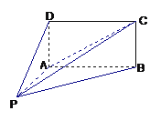
(I)平面PAD与平面PAB是否垂直?并说明理由;
(II)求平面PCD与平面ABCD所成二面角的余弦值.
【答案】(I)平面![]()
![]() 平面
平面![]() ; (Ⅱ) cos∠PEF=
; (Ⅱ) cos∠PEF=![]() .
.
【解析】
(1)说明![]() ,而
,而![]() ,
,![]() ,即可说明平面PAD与平面PAB垂直;(2)以点A为坐标原点,AB所在的直线为y轴建立空间直角坐标系,求出
,即可说明平面PAD与平面PAB垂直;(2)以点A为坐标原点,AB所在的直线为y轴建立空间直角坐标系,求出![]() ,
,![]() ,
,![]() ,进而求出
,进而求出![]() ,
, ![]() ,计算平面PCD的法向量为
,计算平面PCD的法向量为![]() ,平面ABCD的一个法向量为
,平面ABCD的一个法向量为![]() ,代入夹角计算公式即可。
,代入夹角计算公式即可。
(I)平面![]()
![]() 平面
平面![]() ;
;
证明:由题意得![]() 且
且![]()
又![]() ,则
,则![]()
则![]() 平面
平面![]() ,
,
故平面![]() 平面
平面![]()
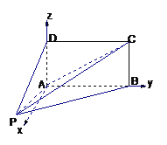
(Ⅱ)以点A为坐标原点,AB所在的直线为y轴建立
空间直角坐标系如右图示,则![]() ,
,![]() ,
,![]()
可得![]() ,
, ![]()
设平面PCD的法向量为![]() ,
,
则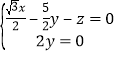 , 令x=2得,
, 令x=2得,![]()
又平面ABCD的一个法向量为![]() ,
,
设平面PCD与平面ABCD所成二面角的大小为θ,显然为锐角θ,
∴cosθ=![]() =
=![]() .
.
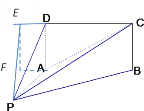
![]() 方法二:过点P作BA的垂线交BA的延长线于点F,过点F 作EF⊥AB,
方法二:过点P作BA的垂线交BA的延长线于点F,过点F 作EF⊥AB,
交CD的延长线于点D.
则∠PEF为平面PCD与平面ABCD所成二面角的平面角
∵PA=1, ∠PAB=120°, ∴PF=![]() ,
,
又EF=AD=PA= 1,∴PE=![]() ,
,
∴cos∠PEF=![]() .
.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3+bx2+cx(x∈R),已知g(x)=f(x)﹣f′(x)是奇函数
(1)求b、c的值.
(2)求g(x)的单调区间与极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,其导函数为f′(x),若f′(x) < f (x),且 f (x+1)=f (3-x),f (2 015)=2,则不等式f (x)<2ex-1的解集为( )
A. (1,+∞) B. (e,+∞) C. (-∞,0) D. (-∞,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某实验室一天的温度(单位:![]() )随时间
)随时间![]() (单位:
(单位:![]() )的变化近似满足函数关系:
)的变化近似满足函数关系:![]() ,
,![]() .
.
(1)求实验室这一天的最高温度;
(2)若要求实验室温度不高于![]() ,则在哪段时间实验室需要降温?
,则在哪段时间实验室需要降温?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在古代三国时期吴国的数学家赵爽创制了一幅“赵爽弦图”,由四个全等的直角三角形围成一个大正方形,中间空出一个小正方形(如图阴影部分)。若直角三角形中较小的锐角为a。现向大正方形区城内随机投掷一枚飞镖,要使飞镖落在小正方形内的概率为![]() ,则
,则![]() _____________。
_____________。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com