
����Ŀ����ƽ��ֱ������ϵxOy�У���֪��ԲS������P����2 ![]() �������붨ԲQ����x��2
�������붨ԲQ����x��2 ![]() ��2+y2=36���У��Ƕ�ԲԲ��S�Ĺ켣Ϊ����C��
��2+y2=36���У��Ƕ�ԲԲ��S�Ĺ켣Ϊ����C��
��1��������C�ķ��̣�
��2��������C��x�ᣬy���������ֱ��ཻ��A��B���㣬��M��NΪ��ԲC����������㣬���е�M�ڵ�һ���ޣ���ֱ��AM��ֱ��BN��б�ʻ�Ϊ�෴�������ж�ֱ��MN��б���Ƿ�Ϊ��ֵ������Ƕ�ֵ��������ֵ��������Ƕ�ֵ��˵�����ɣ�
��3���ڣ�2�������£����ı���AMBN�����ȡֵ��Χ��
���𰸡�
��1���⣺��ԲS�İ뾶ΪR��
�ߵ� ![]() ��Բ
��Բ ![]() �ڣ�����Բ����
�ڣ�����Բ����
����PS=R��QS=6��R��
�� ![]() ��
��
��Բ��S�Ĺ켣Ϊ��P��QΪ���㣬���᳤Ϊ6����Բ
��2a=6��2c=4 ![]() ����a=3��c=2
����a=3��c=2 ![]() ����b2=1��
����b2=1��
������C�ķ���Ϊ ![]()
��2���⣺�ɣ�1����֪A��3��0����B��0��1��
��AM��б��Ϊk����ֱ��AM����Ϊy=k��x��3����ֱ��BN����Ϊy=��kx+1
�� ![]() ����M������Ϊ
����M������Ϊ ![]() ��
��
�� ![]() ����
���� ![]()
����MN��� 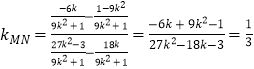
��3���⣺��MN�ķ���Ϊ ![]() ��
��
�� 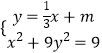 ����2x2+6mx+9m2��9=0
����2x2+6mx+9m2��9=0
�� ![]() ��
��
![]()
A��ֱ��MN�ľ���ֱ�Ϊ ![]()
B��ֱ��MN�ľ���ֱ�Ϊ ![]()
�����ı���AMBN��� ![]() =
= ![]()
�֩�1��m��1�������ı���AMBN�����ȡֵ��Χ�� ![]()
����������1��������Բ���пɵó�P S + Q S = P Q�������õ�Բ��S�Ĺ켣Ϊ��P��QΪ���㣬���᳤Ϊ6����Բ��������֪�����Բ�ķ��̡���2����б��ʽ�������ֱ�ߵķ��̣�������������Բ�ķ��̣����M��N��������꣬�������MN��б�ʡ���3������ֱ�ߺ���Բ�ķ��̣���ȥy�õ�����x�ķ���2x2+6mx+9m2��9=0������Τ�ﶨ������� x M+ x N ��xM .xN �ı���ʽ���ֱ����MN���Լ�A��ֱ��MN�ľ���ֱ�Ϊ d1 ��B��ֱ��MN�ľ���ֱ�Ϊ d2���������ı���AMBN��� S = S �� AMN + S �� BMN=![]() M N ( d 1 + d 2 ),�ٸ���m��ȡֵ��Χ�����õ�����AMBN�����ȡֵ��Χ��
M N ( d 1 + d 2 ),�ٸ���m��ȡֵ��Χ�����õ�����AMBN�����ȡֵ��Χ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��R������f��x��=log2�� ![]() +a����
+a����
��1����a=5ʱ���ⲻ��ʽf��x����0��
��2��������x�ķ���f��x����log2[��a��4��x+2a��5]=0�Ľ⼯��ǡ����һ��Ԫ�أ���a��ȡֵ��Χ��
��3����a��0����������t��[ ![]() ��1]������f��x��������[t��t+1]�ϵ����ֵ����Сֵ�IJ����1����a��ȡֵ��Χ��
��1]������f��x��������[t��t+1]�ϵ����ֵ����Сֵ�IJ����1����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��ȤζУ�˶���İ佱��ʽ��,��һ���߶������������������ֱ�Ϊ120�ˡ�120�ˡ�n��.Ϊ�˻�Ծ����,�����ί���ڰ佱�����д���齱�,���÷ֲ�����ķ����������������й���ȡ20����ǰ�ž���,���и߶���������6��.

(1)��n��ֵ;
(2)����ǰ�ž����ĸ߶�������6�˷ֱ��Ϊa,b,c,d,e,f,��������г�ȡ2����̨�齱.��a��b������һ����̨�齱�ĸ���;
(3)�齱��Ĺ�����:����ͨ����������ʹ�����Զ���������[0,1]֮��ľ��������x,y,������ͼ��ʾ�ij����ͼִ��.��������ʾ���н���,��ô����н�;��������ʾ��лл��,���н�,��ô����н��ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() Ϊ�溯����
Ϊ�溯����![]() Ϊʵ������
Ϊʵ������
��1����![]() ��ֵ��
��ֵ��
��2��֤����![]() ������
������![]() �ڵ���������
�ڵ���������
��3������������![]() �ϵ�ÿһ��
�ϵ�ÿһ��![]() ��ֵ������ʽ
��ֵ������ʽ![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxoy�У���֪������ԭ�㣬������x���ϵ�˫����C��������Ϊ ![]() ����˫����C��б��Ϊ2��ֱ��l�ཻ��������һ������ΪP����3��0����
����˫����C��б��Ϊ2��ֱ��l�ཻ��������һ������ΪP����3��0����
��1����˫����C�ķ��̼����Ľ����߷��̣�
��2������ֱ��l��������Ľ���Ϊ����������ߵı����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
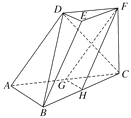
����Ŀ����ͼ������̨DEF ABC����AB��2DE��G��H�ֱ�ΪAC��BC���е㣮
(1)��֤��ƽ��ABED��ƽ��FGH��
(2)��CF��BC��AB��BC����֤��ƽ��BCD��ƽ��EGH.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���������ס������ֲ�Ʒ��������ֱ�Ϊ![]() ��
��![]() ����Ԫ����������Ͷ���ʽ�
����Ԫ����������Ͷ���ʽ�![]() ����Ԫ���Ĺ�ϵ�о��鹫ʽ
����Ԫ���Ĺ�ϵ�о��鹫ʽ![]() ��
��![]() ����150��Ԫ�ʽ�Ͷ�������ס������ֲ�Ʒ����Ҫ��Լס������ֲ�Ʒ��Ͷ�ʽ�����25��Ԫ��
����150��Ԫ�ʽ�Ͷ�������ס������ֲ�Ʒ����Ҫ��Լס������ֲ�Ʒ��Ͷ�ʽ�����25��Ԫ��
��1������Ҳ�ƷͶ���ʽ�![]() ��Ԫ����������
��Ԫ����������![]() ����Ԫ������
����Ԫ������![]() �ĺ�����ϵʽ���䶨����
�ĺ�����ϵʽ���䶨����
��2����η���ʹ���ʽ𣬲���ʹ��������������������Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������R�ϵĺ���f��x�����㣺y=f��x��1����ͼ����ڣ�1��0����Գƣ��ҵ�x��0ʱ����f��x�� ![]() ��=f��x+
��=f��x+ ![]() ������x��[0��2��ʱ��f��x��=ex��1����f��2017��+f����2016��=�� ��
������x��[0��2��ʱ��f��x��=ex��1����f��2017��+f����2016��=�� ��
A.1��e
B.��1��e
C.e��1
D.e+1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���й�Ʊ��30����ÿ�ɵĽ��۸�![]() ��Ԫ����ʱ��
��Ԫ����ʱ��![]() ���죩��������
���죩��������![]() ����
����![]() �����ҷ�ͼ���е������߶��ϣ��ù�Ʊ��30���ڣ�����30�죩���ս�����
�����ҷ�ͼ���е������߶��ϣ��ù�Ʊ��30���ڣ�����30�죩���ս�����![]() ����ɣ���ʱ��
����ɣ���ʱ��![]() ���죩�ĺ�����ϵΪ��
���죩�ĺ�����ϵΪ�� ![]() ��
�� ![]() ��
�� ![]()
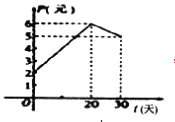
��1�������ṩ��ͼ��д�����ֹ�Ʊÿ�ɵĽ��۸�![]() ��Ԫ����ʱ��
��Ԫ����ʱ��![]() ���죩������ĺ�����ϵʽ��
���죩������ĺ�����ϵʽ��
��2����![]() ����Ԫ����ʾ�ù�Ʊ�ս��д��
����Ԫ����ʾ�ù�Ʊ�ս��д��![]() ����
����![]() �ĺ�����ϵʽ���������30���еڼ����ս���������ֵΪ���٣�
�ĺ�����ϵʽ���������30���еڼ����ս���������ֵΪ���٣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com