
【题目】“开门大吉”是某电视台推出的游戏益智节目.选手面对![]() 号
号![]() 扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金.(奖金金额累加)但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:
扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金.(奖金金额累加)但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:![]() ;
;![]() (单位:岁),其猜对歌曲名称与否人数如图所示.
(单位:岁),其猜对歌曲名称与否人数如图所示.
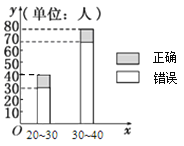
(1)写出![]() 列联表:判断是否有
列联表:判断是否有![]() 的把握认为猜对歌曲名称与否与年龄有关?
的把握认为猜对歌曲名称与否与年龄有关?
说明你的理由.(下面的临界值表供参考)

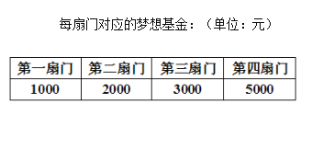
(2)若某选手能正确回答第一、二、三、四扇门的概率分别为![]() ,
,![]() ,
,![]() ,
,![]() ,正确回答一个问题后,选择继续回答下一个问题的概率是
,正确回答一个问题后,选择继续回答下一个问题的概率是![]() ,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为
,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
(参考公式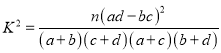 其中
其中![]() )
)
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,且函数
,且函数![]() 的最小正周期为
的最小正周期为![]() 。
。
(1)若函数![]() 在
在![]() 处取到最小值
处取到最小值![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)若将函数![]() 图象上所有点的横坐标伸长到原来的
图象上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变),再将向左平移
倍(纵坐标不变),再将向左平移![]() 个单位,得到的函数图象关于
个单位,得到的函数图象关于![]() 轴对称,求函数
轴对称,求函数![]() 的单调递增区间。
的单调递增区间。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率是![]() ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率是
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率是![]() ,甲、乙两台机床加工的零件都是一等品的概率是
,甲、乙两台机床加工的零件都是一等品的概率是![]() .
.
(1)分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(2)从甲、乙、丙三台机床加工的零件中各取一个检验,求至少有一个一等品的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】7人站成一排.(写出必要的过程,结果用数字作答)
(1)甲、乙两人相邻的排法有多少种?
(2)甲、乙两人不相邻的排法有多少种?
(3)甲、乙、丙三人两两不相邻的排法有多少种?
(4)甲、乙、丙三人至多两人不相邻的排法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取了40辆汽车在经过路段上某点是的车速(![]() ),现将其分成六段:
),现将其分成六段:![]() ,
,
![]() 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.
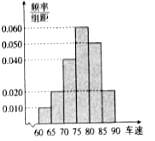
(I)现有某汽车途经该点,则其速度低于80![]() 的概率约是多少?
的概率约是多少?
(II)根据频率分布直方图,抽取的40辆汽车经过该点的平均速度是多少?
(III)在抽取的40辆汽车且速度在![]() (
(![]() )内的汽车中任取2辆,求这2辆车车速都在
)内的汽车中任取2辆,求这2辆车车速都在![]() (
(![]() )内的概率.
)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:![]() ,
,![]() ,…,
,…,![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图:

(1)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间![]() 内的人数;
内的人数;
(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等,试估计总体中男生和女生人数的比例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长时间用手机上网严重影响着学生的身体健康,某校为了解![]() 两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中茎叶表示十位数字,叶表示个位数字).
两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中茎叶表示十位数字,叶表示个位数字).
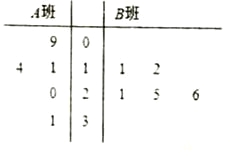
(1)分别求出图中所给两组样本数据的平均值,并据此估计,哪个班的学生平均上网时间较长;
(2)从![]() 班的样本数据中随机抽取一个不超过19的数据记为
班的样本数据中随机抽取一个不超过19的数据记为![]() ,从
,从![]() 班的样本数据中随机抽取一个不超过21的数据记为
班的样本数据中随机抽取一个不超过21的数据记为![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com