
【题目】改革开放40多年来,城乡居民生活从解决温饱的物质需求为主逐渐转变到更多元化的精神追求,消费结构明显优化.下图给出了1983~2017年部分年份我国农村居民人均生活消费支出与恩格尔系数(恩格尔系数是食品支出总额占个人消费支出总额的比重)统计图.对所列年份进行分析,则下列结论错误的是( )
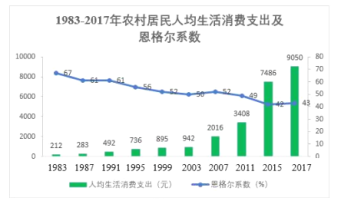
A.农村居民人均生活消费支出呈增长趋势
B.农村居民人均食品支出总额呈增长趋势
C.2011年至2015年农村居民人均生活消费支出增长最快
D.2015年到2017年农村居民人均生活消费支出增长比率大于人均食品支出总额增长比率
【答案】D
【解析】
根据图表数据进行判断,求增长速度,增长率,进行判断.
从图中可以看出,农村居民人均生活消费支出呈增长趋势,故A正确;
根据“农村居民人均食品支出总额![]() 农村居民人均生活消费支出
农村居民人均生活消费支出![]() 恩格尔系数”,
恩格尔系数”,
计算可得农村居民人均食品支出总额呈增长趋势,故B正确;
年 份 | 1983 | 1987 | 1991 | 1995 | 1999 | 2003 | 2007 | 2011 | 2015 | 2017 |
农村居民人均生活消费支出 | 212 | 283 | 492 | 736 | 895 | 942 | 2016 | 3408 | 7486 | 9050 |
恩格尔系数 | 67 | 61 | 61 | 56 | 52 | 50 | 52 | 49 | 42 | 43 |
农村居民人均食品支出总额 | 142.0 | 172.6 | 412.2 | 465.4 | 471 | 1048.3 | 1669.9 | 3144.1 | 3891.5 | |
农村居民人均生活消费支出比较上一统计数据的增长量 | 71 | 209 | 244 | 159 | 47 | 1074 | 1392 | 4078 | 1564 |
2011年至2015年农村居民人均生活消费支出增长4078元,为最快;故C正确;
2015年到2017年农村居民人均生活消费支出增长比率为![]() ,
,
人均食品支出7486总额增长比率为![]() ,故D错误.
,故D错误.
故选:D.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】阳马和鳖臑(bienao)是《九章算术·商功》里对两种锥体的称谓.如图所示,取一个长方体,按下图斜割一分为二,得两个模一样的三棱柱,称为堑堵(如图).再沿其中一个堑堵的一个顶点与相对的棱剖开,得四棱锥和三棱锥各一个,有一棱与底面垂直的四棱锥称为阳马(四棱锥![]() )余下三棱锥称为鳖臑(三棱锥
)余下三棱锥称为鳖臑(三棱锥![]() )若将某长方体沿上述切割方法得到一个阳马一个鳖臑,且该阳马的正视图和鳖臑的侧视图如图所示,则可求出该阳马和鳖臑的表面积之和为( )
)若将某长方体沿上述切割方法得到一个阳马一个鳖臑,且该阳马的正视图和鳖臑的侧视图如图所示,则可求出该阳马和鳖臑的表面积之和为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某校打算在长为1千米的主干道![]() 一侧的一片区域内临时搭建一个强基计划高校咨询和宣传台,该区域由直角三角形区域
一侧的一片区域内临时搭建一个强基计划高校咨询和宣传台,该区域由直角三角形区域![]() (
(![]() 为直角)和以
为直角)和以![]() 为直径的半圆形区域组成,点
为直径的半圆形区域组成,点![]() (异于
(异于![]() ,
,![]() )为半圆弧上一点,点
)为半圆弧上一点,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .已知
.已知![]() ,设
,设![]() ,且
,且![]() .初步设想把咨询台安排在线段
.初步设想把咨询台安排在线段![]() ,
,![]() 上,把宣传海报悬挂在弧
上,把宣传海报悬挂在弧![]() 和线段
和线段![]() 上.
上.
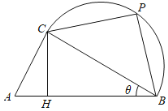
(1)若为了让学生获得更多的咨询机会,让更多的省内高校参展,打算让![]() 最大,求该最大值;
最大,求该最大值;
(2)若为了让学生了解更多的省外高校,贴出更多高校的海报,打算让弧![]() 和线段
和线段![]() 的长度之和最大,求此时的
的长度之和最大,求此时的![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】折纸是一项艺术,可以折出很多数学图形.将一张圆形纸片放在平面直角坐标系中,圆心B(-1,0),半径为4,圆内一点A为抛物线![]() 的焦点.若每次将纸片折起一角,使折起部分的圆弧的一点
的焦点.若每次将纸片折起一角,使折起部分的圆弧的一点![]() 始终与点A重合,将纸展平,得到一条折痕,设折痕与线段
始终与点A重合,将纸展平,得到一条折痕,设折痕与线段![]() B的交点为P.
B的交点为P.
(Ⅰ)将纸片展平后,求点P的轨迹C的方程;
(Ⅱ)已知过点A的直线l与轨迹C交于R,S两点,当l无论如何变动,在AB所在直线上存在一点T,使得![]() 所在直线一定经过原点,求点T的坐标.
所在直线一定经过原点,求点T的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,要利用一半径为![]() 的圆形纸片制作三棱锥形包装盒.已知该纸片的圆心为
的圆形纸片制作三棱锥形包装盒.已知该纸片的圆心为![]() ,先以
,先以![]() 为中心作边长为
为中心作边长为![]() (单位:
(单位:![]() )的等边三角形
)的等边三角形![]() ,再分别在圆
,再分别在圆![]() 上取三个点
上取三个点![]() ,
,![]() ,
,![]() ,使
,使![]() ,
,![]() ,
,![]() 分别是以
分别是以![]() ,
,![]() ,
,![]() 为底边的等腰三角形.沿虚线剪开后,分别以
为底边的等腰三角形.沿虚线剪开后,分别以![]() ,
,![]() ,
,![]() 为折痕折起
为折痕折起![]() ,
,![]() ,
,![]() ,使得
,使得![]() ,
,![]() ,
,![]() 重合于点
重合于点![]() ,即可得到正三棱锥
,即可得到正三棱锥![]() .
.
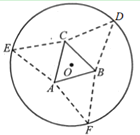

(1)若三棱锥![]() 是正四面体,求
是正四面体,求![]() 的值;
的值;
(2)求三棱锥![]() 的体积
的体积![]() 的最大值,并指出相应
的最大值,并指出相应![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,x轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线C的极坐标方程为![]() ,直线l的参数方程为
,直线l的参数方程为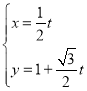 ,(t为参数).
,(t为参数).
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C交于A,B两点,![]() ,且
,且![]() ,求
,求![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,a1=1,an>0,Sn2=an+12﹣λSn+1,其中λ为常数.
(1)证明:Sn+1=2Sn+λ;
(2)是否存在实数λ,使得数列{an}为等比数列,若存在,求出λ;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
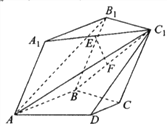
【题目】在如图所示的多面体中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为边长为2的菱形,
为边长为2的菱形, ![]() 为直角梯形,四边形
为直角梯形,四边形![]() 为平行四边形,且
为平行四边形,且![]() ,
, ![]() ,
, ![]() .
.
(1)若![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,
, ![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com