Question

若等差数列{a_n}中，公差d=2，且a₁+a₂+…+a₁₀₀=200，则a₅+a₁₀+a₁₅+…+a₁₀₀的值是     ．

Answer 1

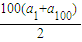
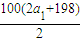
【答案】分析：由a₁+a₂+…+a₁₀₀=200可知，s₁₀₀===200，求出a₁得到a_n的通项，a₅+a₁₀+a₁₅+…+a₁₀₀为等差数列，求出首项和公差即可求出之和．
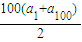
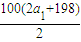
解答：解：因为s₁₀₀===200，所以a₁=-97，则a_n=2n-99，
而a₅，a₁₀，a₁₅，…，a₁₀₀为首项为-89，公差为10的等差数列，项数是20，
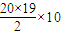
则a₅+a₁₀+a₁₅+…+a₁₀₀=20×（-89）+=120
故答案为120
点评：考查学生灵活运用等差数列的前n项和的公式，灵活运用等差数列性质的能力．