
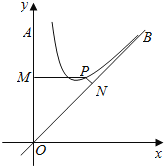
【题目】如图,![]() 是南北方向的一条公路,
是南北方向的一条公路,![]() 是北偏东
是北偏东![]() 方向的一条公路,某风景区的一段边界为曲线
方向的一条公路,某风景区的一段边界为曲线![]() .为方便游客光,拟过曲线
.为方便游客光,拟过曲线![]() 上的某点分别修建与公路
上的某点分别修建与公路![]() ,
,![]() 垂直的两条道路
垂直的两条道路![]() ,
,![]() ,且
,且![]() ,
,![]() 的造价分别为5万元
的造价分别为5万元![]() 百米,40万元
百米,40万元![]() 百米,建立如图所示的直角坐标系
百米,建立如图所示的直角坐标系![]() ,则曲线符合函数
,则曲线符合函数![]() 模型,设
模型,设![]() ,修建两条道路
,修建两条道路![]() ,
,![]() 的总造价为
的总造价为![]() 万元,题中所涉及的长度单位均为百米.
万元,题中所涉及的长度单位均为百米.
(1)求![]() 解析式;
解析式;
(2)当![]() 为多少时,总造价
为多少时,总造价![]() 最低?并求出最低造价.
最低?并求出最低造价.
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 以
以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,设点
轴正半轴为极轴建立极坐标系,设点![]() 在曲线
在曲线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,且
上,且![]() 为正三角形.
为正三角形.
(1)求点![]() ,
,![]() 的极坐标;
的极坐标;
(2)若点![]() 为曲线
为曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家统计局服务业调查中心和中国物流与采购联合会发布的2018年10月份至2019年9月份共12个月的中国制造业采购经理指数(PMI)如下图所示.则下列结论中错误的是( )
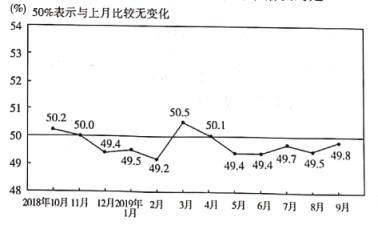
A.12个月的PMI值不低于50%的频率为![]()
B.12个月的PMI值的平均值低于50%
C.12个月的PMI值的众数为49.4%
D.12个月的PMI值的中位数为50.3%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,则关于x的方程
,则关于x的方程![]() 有以下结论,其中正确的结论为( )
有以下结论,其中正确的结论为( )
A.当![]() 时,方程
时,方程![]() 恒有实根
恒有实根
B.当![]() 时,方程
时,方程![]() 在
在![]() 内有两个不等实根
内有两个不等实根
C.当![]() 时,方程
时,方程![]() 在
在![]() 内最多有9个不等实根
内最多有9个不等实根
D.若方程![]() 在
在![]() 内的实根的个数为偶数,则所有实根之和为
内的实根的个数为偶数,则所有实根之和为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正三棱柱![]() (底面是正三角形,侧棱垂直底面)的各条棱长均相等,
(底面是正三角形,侧棱垂直底面)的各条棱长均相等,![]() 为
为![]() 的中点,
的中点,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的动点(含端点),且满足
上的动点(含端点),且满足![]() .当
.当![]() 、
、![]() 运动时,下列结论中正确的个数是( )
运动时,下列结论中正确的个数是( )
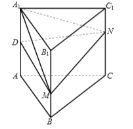
①平面![]() 平面
平面![]() ;
;
②三棱锥![]() 的体积为定值;
的体积为定值;
③![]() 可能为直角三角形;
可能为直角三角形;
④平面![]() 与平面
与平面![]() 所成的锐二面角范围为
所成的锐二面角范围为![]() .
.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知坐标平面上动点![]() 与两个定点
与两个定点![]() ,
, ![]() ,且
,且![]() .
.
(1)求点![]() 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中轨迹为![]() ,过点
,过点![]() 的直线
的直线![]() 被
被![]() 所截得的线段长度为8,求直线
所截得的线段长度为8,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,已知点
中,已知点![]() 在直线
在直线![]() 上运动,则下列四个命题中:①三棱锥
上运动,则下列四个命题中:①三棱锥![]() 的体积不变;②
的体积不变;②![]() ;③当
;③当![]() 为
为![]() 中点时,二面角
中点时,二面角![]() 的余弦值为
的余弦值为![]() ;④若正方体的棱长为2,则
;④若正方体的棱长为2,则![]() 的最小值为
的最小值为![]() ;其中说法正确的是____________(写出所有说法正确的编号)
;其中说法正确的是____________(写出所有说法正确的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (a,b
(a,b![]() R)的导函数为
R)的导函数为![]() ,已知
,已知![]() ,
,![]() 是
是![]() 的两个不同的零点.
的两个不同的零点.
(1)证明:![]() ;
;
(2)当b=0时,若对任意x>0,不等式![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(3)求关于x的方程![]() 的实根的个数.
的实根的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com