
【题目】某公司准备上市一款新型轿车零配件,上市之前拟在其一个下属4S店进行连续30天的试销.定价为1000元/件.试销结束后统计得到该4S店这30天内的日销售量(单位:件)的数据如下表:
日销售量 | 40 | 60 | 80 | 100 |
频数 | 9 | 12 | 6 | 3 |
(1)若该4S店试销期间每个零件的进价为650元/件,求试销连续30天中该零件日销售总利润不低于24500元的频率;
(2)试销结束后,这款零件正式上市,每个定价仍为1000元,但生产公司对该款零件不零售,只提供零件的整箱批发,大箱每箱有60件,批发价为550元/件;小箱每箱有45件,批发价为600元/件.该4S店决定每天批发两箱,根据公司规定,当天没销售出的零件按批发价的9折转给该公司的另一下属4S店.假设该4店试销后的连续30天的日销售量(单位:件)的数据如下表:
日销售量 | 50 | 70 | 90 | 110 |
频数 | 5 | 15 | 8 | 2 |
(ⅰ)设该4S店试销结束后连续30天每天批发两大箱,这30天这款零件的总利润;
(ⅱ)以总利润作为决策依据,该4S店试销结束后连续30天每天应该批发两大箱还是两小箱?
【答案】(1)![]() (2)(ⅰ)
(2)(ⅰ)![]() 万元(ⅱ)每天应该批发两大箱
万元(ⅱ)每天应该批发两大箱
【解析】
(1)求出日销售总利润不低于24500元所需的日销售件数,得出符合要求的天数,可求对应频率;
(2)每天的利润等于销售额加九折的转让费减成本,分别算出两大箱和两小箱30天的总利润作比较.
解:(1)∵试销期间每个零件的利润为![]() 元,
元,
所以要使得日销售总利润不低于24500元,则日销售零件的件数不能少于![]() ,
,
∴所求频率为![]() .
.
(2)(ⅰ)批发两大箱,则批发成本为![]() 元,
元,
当日销售量为50件时,
当日利润为![]() 元;
元;
当日销售量为70件时,
当日利润为![]() 元;
元;
当日销售量为90件时,
当日利润为![]() 元;
元;
当日销售量量为110件时,
当日利润为![]() 元;
元;
所以这30天这款零件的总利润为
![]() 万元.
万元.
(ⅱ)若批发两小箱,则批发成本为![]() 元,
元,
当日销售量为50件时,
当日利润为![]() 元;
元;
当日销售量为70件时,
当日利润为![]() 元;
元;
当日销售量为90件或110件时,
当日利润为![]() 元.
元.
所以这30天这款零件的总利润为
![]() 万元,
万元,
∵93.32万元![]() 万元,
万元,
∴每天应该批发两大箱.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案科目:高中数学 来源: 题型:
【题目】袋子中有大小、形状完全相同的四个小球,分别写有和、“谐”、“校”“园”四个字,有放回地从中任意摸出一个小球,直到“和”、“谐”两个字都摸到就停止摸球,用随机模拟的方法估计恰好在第三次停止摸球的概率。利用电脑随机产生![]() 到
到![]() 之间取整数值的随机数,分别用
之间取整数值的随机数,分别用![]() ,
,![]() ,
,![]() ,
,![]() 代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下
代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下![]() 组随机数:
组随机数:
![]()
由此可以估计,恰好第三次就停止摸球的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】港珠澳大桥是中国建设史上里程最长,投资最多,难度最大的跨海桥梁项目,大桥建设需要许多桥梁构件。从某企业生产的桥梁构件中抽取![]() 件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间
件,测量这些桥梁构件的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.
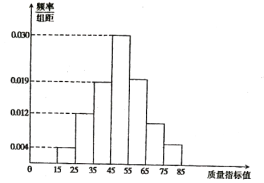
(1)求这些桥梁构件质量指标值落在区间![]() 内的频率;
内的频率;
(2)用分层抽样的方法在区间![]() 内抽取一个容量为
内抽取一个容量为![]() 的样本,将该样本看成一个总体,从中任意抽取
的样本,将该样本看成一个总体,从中任意抽取![]() 件桥梁构件,求这
件桥梁构件,求这![]() 件桥梁构件都在区间
件桥梁构件都在区间![]() 内的概率
内的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人轮流吹同一只气球,当且仅当气球内的气体体积![]() (单位:毫升)大于2014时,气球会被吹破.先由甲开始吹入1毫升气体,约定以后每次吹入的气体体积为上一次体积的2倍或
(单位:毫升)大于2014时,气球会被吹破.先由甲开始吹入1毫升气体,约定以后每次吹入的气体体积为上一次体积的2倍或![]() ,且吹入的气体体积为整数.
,且吹入的气体体积为整数.
(1)若谁先吹破气球谁输,问谁有必胜策略?证明你的结论.
(2)若在不吹破气球的前提下,约定单次吹入的气体体积最大者为赢家(如果吹入的体积相同,则最先吹出最大体积者为赢家).问:谁有必胜策略?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】证明:存在无数个满足如下条件的整数組(a,b,c,d):
(1)a>c>0,(a,c)=1;
(2)对任意给定的正整数k,恰有k个正整数n,使得(an+b)|(cn+d)。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】擎天柱为了防止魔方落入霸天虎手中,打算用激光刀将其销毁.擎天柱使用的方法是:每次切割可将魔方分成两个体积之比为![]() 的六面体,每个六面体恰包含魔方的一个面,且任两次操作得到的截面在魔方中均有交点,而魔方的属性决定每次切割只能暂时将它割开,而无法分离,且只要它有
的六面体,每个六面体恰包含魔方的一个面,且任两次操作得到的截面在魔方中均有交点,而魔方的属性决定每次切割只能暂时将它割开,而无法分离,且只要它有![]() 的小正方体区域始终未被割到,就无法被销毁,证明:无论擎天柱切割多少次,均无法销毁魔方.
的小正方体区域始终未被割到,就无法被销毁,证明:无论擎天柱切割多少次,均无法销毁魔方.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() ,下列对函数
,下列对函数![]() 的性质描述正确的是( )
的性质描述正确的是( )
A.函数![]() 的图象关于点
的图象关于点![]() 对称
对称
B.若![]() ,则函数f(x)有极值点
,则函数f(x)有极值点
C.若![]() ,函数
,函数![]() 在区间
在区间![]() 单调递减
单调递减
D.若函数![]() 有且只有3个零点,则a的取值范围是
有且只有3个零点,则a的取值范围是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com