
(1)画出这个空间直角坐标系并求出直线AB与x轴所成的较小的角;
(2)若M为BC的中点,n=![]() m,求直线AM与PM所成锐角.
m,求直线AM与PM所成锐角.
解:(1)根据已知条件,画空间直角坐标系如图4.

图4
以射线AC为y轴正方向,射线AP为z轴正方向,A为坐标原点建立空间直角坐标系O—xyz,过点B作BE⊥Ox,垂足为E,则
因为B(![]() m,m,0),所以E(
m,m,0),所以E(![]() m,0,0),
m,0,0),
在Rt△AEB中,∠AEB=90°,|AE|=![]() m,|EB|=m,
m,|EB|=m,
∴tan∠BAE=![]() .∴∠BAE=30°,
.∴∠BAE=30°,
即直线AB与x轴所成的较小的角为30°.
(2)连接AM和PM,∵M(x,y,z)为BC的中点,且B(![]() m,m,0),C(0,2m,0),由中点坐标公式可得x=
m,m,0),C(0,2m,0),由中点坐标公式可得x=![]() ,y=
,y=![]() ,z=
,z=![]() =0,∴M(
=0,∴M(![]() ,
,![]() ,0).
,0).
∵A(0,0,0),∴由两点间的距离公式得|AM|=![]() =
=![]() m.
m.
∵P(0,0,2n)且n=![]() m,∴P(0,0,
m,∴P(0,0,![]() m).∴|OP|=
m).∴|OP|=![]() m,故|OP|=|AM|.
m,故|OP|=|AM|.
∵∠PAM=90°,
∴∠PMA=45°,即直线AM与PM所成锐角为45°.


科目:高中数学 来源: 题型:
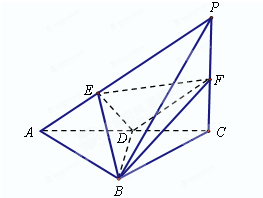 已知三棱锥P-ABC中,PC⊥底面ABC,AB=BC,D、F分别为AC、PC的中点,DE⊥AP于E.
已知三棱锥P-ABC中,PC⊥底面ABC,AB=BC,D、F分别为AC、PC的中点,DE⊥AP于E.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知三棱锥P-ABC,∠ACB=90°,CB=4,AB=20,D为AB中点,M为PB的中点,且△PDB是正三角形,PA⊥PC.
如图,已知三棱锥P-ABC,∠ACB=90°,CB=4,AB=20,D为AB中点,M为PB的中点,且△PDB是正三角形,PA⊥PC.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2009•河西区二模)如图,已知三棱锥P-ABC中,PA⊥面ABC,其中正视图为Rt△PAC,AC=2
(2009•河西区二模)如图,已知三棱锥P-ABC中,PA⊥面ABC,其中正视图为Rt△PAC,AC=2| 6 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2009•黄浦区二模)已知三棱锥P-ABC的棱长都是2,点D是棱AP上不同于P的点.
(2009•黄浦区二模)已知三棱锥P-ABC的棱长都是2,点D是棱AP上不同于P的点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com