
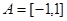 ,
,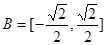 ,函数
,函数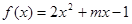 ,
,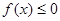 的解集为C,当
的解集为C,当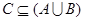 时,求实数
时,求实数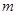 取值范围;
取值范围;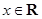 ,都有
,都有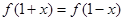 成立,求
成立,求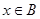 时,
时,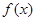 的值域;
的值域;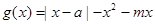
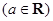 ,求
,求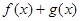 的最小值.
的最小值. (2)
(2)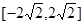 (3)
(3)
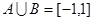 ,因为
,因为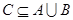 ,
, 图像开口向上,
图像开口向上, 恒成立,故图像始终与
恒成立,故图像始终与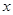 轴有两个交点,由题意,要使这两个交点横坐标
轴有两个交点,由题意,要使这两个交点横坐标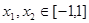 ,当且仅当:
,当且仅当: ,………3分,解得:
,………3分,解得: ……4分
……4分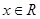 都有
都有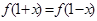 ,所以
,所以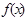 图像关于直线
图像关于直线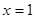 对称,所以
对称,所以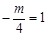 ,
,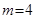 .所以
.所以 为
为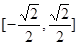 上减函数.
上减函数. 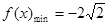 ;
; .故
.故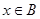 时,
时,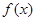 值域为
值域为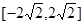 6分(3)令
6分(3)令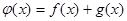 ,则
,则
 时,
时, ,当
,当 ,
,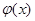 在
在 上单调递减,从而函数
上单调递减,从而函数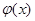 在
在 上的最小值为
上的最小值为 .
. ,则函数
,则函数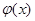 在
在 上的最小值为
上的最小值为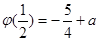 ,且
,且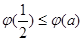
 时,函数
时,函数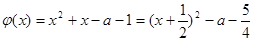 ,若
,若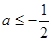 ,
,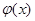 在
在 上的最小值为
上的最小值为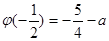 ,且
,且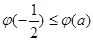 ,若
,若 ,
,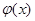 在
在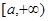 上单调递增,
上单调递增,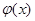 在
在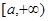 上的最小值为
上的最小值为 .…………………………1分
.…………………………1分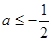 时,函数
时,函数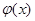 的最小值为
的最小值为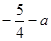 ,当
,当 时,
时,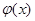 的最小值为
的最小值为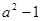
 时,函数
时,函数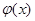 的最小值为
的最小值为 . 13分GH
. 13分GH

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com