
分析 (1)求出圆的半径,即可求圆N的方程;
(2)根据题意得到直线l斜率存在,设为k,表示出直线l方程,利用点到直线的距离公式表示出圆心到直线l的距离d,根据r与弦长,利用垂径定理及勾股定理列出关于k的方程,求出方程的解得到k的值即可.
解答 解:(1)设圆N的方程为(x-3)2+(y-4)2=r2,
由题意知r=3,∴圆N的方程为(x-3)2+(y-4)2=9;
(2)设直线l方程为y-6=k(x-3),即kx-y-3k+6=0,
∵圆心(3,4)到直线l的距离d=$\frac{2}{\sqrt{1+{k}^{2}}}$,r=3,弦长为4$\sqrt{2}$,
得${({2\sqrt{2}})^2}={r^2}-{d^2}$,化简得1+k2=4,即$k=±\sqrt{3}$…(10分)
点评 此题考查了直线与圆相交的性质,涉及的知识有:点到直线的距离公式,圆的标准方程,垂径定理,以及勾股定理,熟练掌握公式及定理是解本题的关键.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:选择题
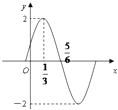 已知函数$f(x)=Asin(ωx+ϕ)(x∈R,A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,则ω,ϕ分别为( )
已知函数$f(x)=Asin(ωx+ϕ)(x∈R,A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,则ω,ϕ分别为( )| A. | ω=π,ϕ=$\frac{π}{6}$ | B. | $ω=2π,ϕ=\frac{π}{6}$ | C. | $ω=π,ϕ=\frac{π}{3}$ | D. | $ω=2π,ϕ=\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 支持 | a= | c= | |
| 不支持 | b= | d= | |
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{2}$或$\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{2}$或$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com