
【题目】已知![]() ,
,![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,且
,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设![]() ,
,![]() ,连接
,连接![]() 并延长,与轨迹
并延长,与轨迹![]() 交于另一点
交于另一点![]() ,点
,点![]() 是
是![]() 中点,
中点,![]() 是坐标原点,记
是坐标原点,记![]() 与
与![]() 的面积之和为
的面积之和为![]() ,求
,求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】随着互联网技术的快速发展,人们更加关注如何高效地获取有价值的信息,网络知识付费近两年呈现出爆发式的增长,为了了解网民对网络知识付费的态度,某网站随机抽查了![]() 岁及以上不足
岁及以上不足![]() 岁的网民共
岁的网民共![]() 人,调查结果如下:
人,调查结果如下:

(1)请完成上面的![]() 列联表,并判断在犯错误的概率不超过
列联表,并判断在犯错误的概率不超过![]() 的前提下,能否认为网民对网络知识付费的态度与年龄有关?
的前提下,能否认为网民对网络知识付费的态度与年龄有关?
(2)在上述样本中用分层抽样的方法,从支持和反对网络知识付费的两组网民中抽取![]() 名,若在上述
名,若在上述![]() 名网民中随机选
名网民中随机选![]() 人,设这
人,设这![]() 人中反对态度的人数为随机变量
人中反对态度的人数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:  ,
, ![]() .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1=![]() ,设bn=
,设bn=![]() ,n∈N*。
,n∈N*。
(1)证明{bn}是等比数列(指出首项和公比);
(2)求数列{log2bn}的前n项和Tn。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点
的中点
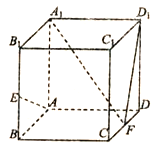
(1)求证:![]() 面
面![]() ;
;
(2)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 面
面![]() ,若存在,试确定
,若存在,试确定![]() 的值,若不存在说明理由;
的值,若不存在说明理由;
(3)在(2)的条件下,求面![]() 与面
与面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲同学写出三个不等式:![]() :
:![]() ,
,![]() :
:![]() ,
,![]() :
:![]() ,然后将
,然后将![]() 的值告诉了乙、丙、丁三位同学,要求他们各用一句话来描述,以下是甲、乙、丙、丁四位同学的描述:
的值告诉了乙、丙、丁三位同学,要求他们各用一句话来描述,以下是甲、乙、丙、丁四位同学的描述:
乙:![]() 为整数;
为整数;
丙:![]() 是
是![]() 成立的充分不必要条件;
成立的充分不必要条件;
丁:![]() 是
是![]() 成立的必要不充分条件;
成立的必要不充分条件;
甲:三位同学说得都对,则![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水葫芦原产于巴西,![]() 年作为观赏植物引入中国. 现在南方一些水域水葫芦已泛滥成灾严重影响航道安全和水生动物生长. 某科研团队在某水域放入一定量水葫芦进行研究,发现其蔓延速度越来越快,经过
年作为观赏植物引入中国. 现在南方一些水域水葫芦已泛滥成灾严重影响航道安全和水生动物生长. 某科研团队在某水域放入一定量水葫芦进行研究,发现其蔓延速度越来越快,经过![]() 个月其覆盖面积为
个月其覆盖面积为![]() ,经过
,经过![]() 个月其覆盖面积为
个月其覆盖面积为![]() . 现水葫芦覆盖面积
. 现水葫芦覆盖面积![]() (单位
(单位![]() )与经过时间
)与经过时间![]() 个月的关系有两个函数模型
个月的关系有两个函数模型![]() 与
与![]() 可供选择.
可供选择.
(参考数据:![]() )
)
(Ⅰ)试判断哪个函数模型更合适,并求出该模型的解析式;
(Ⅱ)求原先投放的水葫芦的面积并求约经过几个月该水域中水葫芦面积是当初投放的![]() 倍.
倍.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com