
����Ŀ���ס�����֧��ӽ����ܾ��������������߳���ʤ�ƣ�������һ����ʤ�ij�����˶�Ϊ�ܹھ��������ʹ˽���.������ʵ���൱��ÿ���������ӻ�ʤ�Ŀ����Ծ�Ϊ![]() .����������ͳ�ƣ���һ�������ɻ����Ʊ����40��Ԫ���Ժ�ÿ��������Ʊ�������һ������10��Ԫ.
.����������ͳ�ƣ���һ�������ɻ����Ʊ����40��Ԫ���Ժ�ÿ��������Ʊ�������һ������10��Ԫ.
(I)���ܾ����л����Ʊ������ǡ��Ϊ300��Ԫ�ĸ��ʣ�
(II)���ܾ����л����Ʊ������ΪX����X�ľ�ֵE(X).
���𰸡�(1) ![]() ��(2)377.5��Ԫ.
��(2)377.5��Ԫ.
�����������������
(1)�������ϵȲ����е����ʿɵ��ܾ�����������5������϶���ֲ���ʽ�ɵ��ܾ����л����Ʊ������ǡ��Ϊ300��Ԫ�ĸ�����![]() ��
��
(2)�������֪�������X��ȡ��ֵΪ220��300��390��490.������������ֵ��ø���ֵ��Ȼ������ֵ�ɵ�E(X)=377.5��Ԫ.
���������
(1)�����⣬ÿ��������õ���Ʊ�����������Ϊ40������Ϊ10�ĵȲ�����.
�������Ϊ{an}������֪a1��40��an��10n��30��
����Sn��![]() ��300.
��300.
���n��5��n����12(��ȥ)�������ܾ�����������5��
��ǰ4�������ıȷֱ�Ϊ1��3���ҵ�5������Ϊ���ȵ���ӻ�ʤ�������Ϊ![]() .
.
�����ܾ����л����Ʊ������ǡ��Ϊ300��Ԫ�ĸ���Ϊ![]() .
.
(2)�������X��ȡ��ֵΪS4��S5��S6��S7����220��300��390��490.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
����X�ķֲ���Ϊ
X | 220 | 300 | 390 | 490 |
P |
|
|
|
|
����X�ľ�ֵΪE(X)��220��![]() ��300��
��300��![]() ��390��
��390��![]() ��490��
��490��![]() ��377.5(��Ԫ).
��377.5(��Ԫ).



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���輯��A={x|1��x��2}��B={x|2a��1��x��2a+1}��
������AB����a��ȡֵ��Χ��
������A��B=����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=loga��1+x����g��x��=loga��1��x�������У�a��0��a��1������h��x��=f��x����g��x����
��1����h��x���Ķ�����
��2���ж�h��x������ż�ԣ���˵�����ɣ�
��3����a=log327+log2����ʹf��x����1������x�ļ��ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪c��0��������p������y��cxΪ������������q����![]() ʱ������
ʱ������![]() ������������p��q��Ϊ�����⣬��p��q��Ϊ�����⣬��c��ȡֵ��Χ��
������������p��q��Ϊ�����⣬��p��q��Ϊ�����⣬��c��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Q(�ѣ���)���ֱ��������������P�ļ����꣮
��1����P�ǵ�Q���ڼ���O�ĶԳƵ㣻
��2����P�ǵ�Q����ֱ�ߦȣ� ![]() �ĶԳƵ㣮
�ĶԳƵ㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��100���{һ�����ֳ�ˮƽ��ͬ�ļס���������ƽ�а���,ÿ��50��.����ʦ����A��B���ֲ�ͬ�Ľ�ѧ��ʽ�ֱ��ڼס��������༶���н̸�ʵ��.Ϊ�˽��ѧЧ��,��ĩ���Ժ�,����ʦ�Լס��������༶��ѧ���ɼ�����ͳ�Ʒ���,����Ƶ�ʷֲ�ֱ��ͼ������ͼ��.�dzɼ�������90����Ϊ���ɼ�������

�� | 0.05 | 0.01 | 0.001 |
�� | 3.841 | 6.635 | 10.828 |
(I)���Ұ������ȡ2��ѧ���ijɼ�,�����ɼ��������ĸ���Ϊ![]() ����
����![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
(II)����Ƶ�ʷֲ�ֱ��ͼ��д����2 x2������,���ж��Ƿ���95���İ�����Ϊ:���ɼ����������ѧ��ʽ�й�.
�װ���A��ʽ�� | �Ұ�(B��ʽ�� | �ܼ� | |
�ɼ����� | |||
�ɼ������� | |||
�ܼ� |
���� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
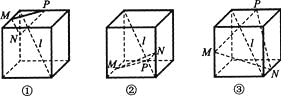
����Ŀ���������������ͼ���У�![]() ���������һ���Խ��ߣ���M��N��P�ֱ�Ϊ����������е㣬���ܵó�
���������һ���Խ��ߣ���M��N��P�ֱ�Ϊ����������е㣬���ܵó�![]() ����MNP��ͼ�ε����(д�����з���Ҫ���ͼ�����)
����MNP��ͼ�ε����(д�����з���Ҫ���ͼ�����)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ԭ�� O ��ֱ����Բ C �� ![]() ��һ������Ϊ P ���� M Ϊ�߶� OP ���е㡣
��һ������Ϊ P ���� M Ϊ�߶� OP ���е㡣
��1����Բ C �ļ����귽�̣�
��2����� M �켣�ļ����귽�̣���˵������ʲô���ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������R�ϵĺ���f��x��= ![]() ��a��R�����溯��������g��x��=
��a��R�����溯��������g��x��= ![]() �Ķ�����Ϊ����1��+�ޣ���
�Ķ�����Ϊ����1��+�ޣ���
��1����a��ֵ��
��2����g��x��= ![]() �ڣ���1��+�ޣ��ϵݼ������ݵ����ԵĶ�����ʵ��m��ȡֵ��Χ��
�ڣ���1��+�ޣ��ϵݼ������ݵ����ԵĶ�����ʵ��m��ȡֵ��Χ��
��3���ڣ�2���������£�������h��x��=f��x��+g��x�������䣨��1��1�������ҽ���������ͬ����㣬��ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com