
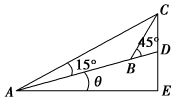
 如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100m到达B处,又测得C对于山坡的斜度为45°,若CD=50m,山坡对于地平面的坡度为θ,则cosθ=$\sqrt{3}$-1.
如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C对于山坡的斜度为15°,向山顶前进100m到达B处,又测得C对于山坡的斜度为45°,若CD=50m,山坡对于地平面的坡度为θ,则cosθ=$\sqrt{3}$-1. 分析 易求∠ACB=30°,在△ABC中,由正弦定理可求BC,在△BCD中,由正弦定理可求sin∠BDC,再由∠BDC=θ+90°可得答案.
解答 解:∵∠CBD=45°,∴∠ACB=30°,
在△ABC中,由正弦定理,得BC=$\frac{100sin15°}{sin30°}$=50($\sqrt{6}$-$\sqrt{2}$),
在△BCD中,由正弦定理,得$\frac{50(\sqrt{6}-\sqrt{2})}{sin∠BDC}=\frac{50}{sin45°}$,
∴sin∠BDC=$\sqrt{3}$-1,即sin(θ+90°)=$\sqrt{3}$-1,
∴cosθ=$\sqrt{3}$-1,
故答案为$\sqrt{3}$-1.
点评 该题考查正弦定理在实际问题中的应用,属基础题,由实际问题恰当构建数学模型是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
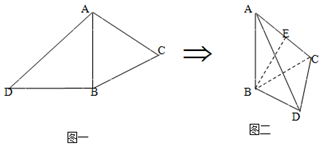 如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2.将△ABD沿AB折起,使得面ABD⊥面ABC,如图二,E为AC的中点
如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2.将△ABD沿AB折起,使得面ABD⊥面ABC,如图二,E为AC的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
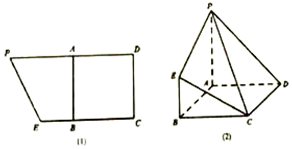 已知梯形CEPD如图(1)所示,其中PD=8,CE=6,A为线段PD的中点,四边形ABCD为正方形,现沿AB进行折叠,使得平面PABE⊥平面ABCD,得到如图(2)所示的几何体.已知当点F满足$\overrightarrow{AF}$=$λ\overrightarrow{AB}$(0<λ<1)时,平面DEF⊥平面PCE,则λ的值为( )
已知梯形CEPD如图(1)所示,其中PD=8,CE=6,A为线段PD的中点,四边形ABCD为正方形,现沿AB进行折叠,使得平面PABE⊥平面ABCD,得到如图(2)所示的几何体.已知当点F满足$\overrightarrow{AF}$=$λ\overrightarrow{AB}$(0<λ<1)时,平面DEF⊥平面PCE,则λ的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{4}{3}$,$\frac{1}{6}$] | B. | (0,$\frac{1}{6}$] | C. | (0,$\frac{1}{6}$) | D. | (-$\frac{4}{3}$,$\frac{1}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
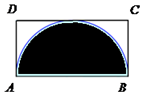 若将一个质点随机投入如图所示的长方形ABCD中,其中AB=2,BC=1,则质点落在以AB为直径的半圆内的概率是( )
若将一个质点随机投入如图所示的长方形ABCD中,其中AB=2,BC=1,则质点落在以AB为直径的半圆内的概率是( )| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{5}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin($-\frac{π}{18}$)>sin($-\frac{π}{10}$) | B. | sin250°>sin260° | C. | tan$\frac{π}{4}$>tan$\frac{π}{6}$ | D. | tan138°>tan143° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com