
【题目】如图,已知点P在☉O外,PC是☉O的切线,切点为C,直线PO与☉O相交于点A,B. 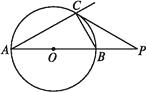
(1)试探索∠BCP与∠P的数量关系;
(2)若∠A=30°,则PB与PA有什么关系?
(3)∠A可能等于45°吗?为什么?
【答案】
(1)解:∵PC是切线,
∴∠BCP=∠A.
又∵AB是直径,
∴∠ACB=90°.
在△ACP中,∠A+∠P+∠ACP=180°,
∴∠BCP+∠P+∠ACB+∠BCP=180°.
∴2∠BCP+∠P+90°=180°.
∴∠P=90°-2∠BCP.
(2)解:若∠A=30°,则∠BCP=∠A=30°,∠ABC=60°.
∴∠P=30°,∴PB=BC,BC= AB.
∴PB= PA,即PA=3PB.
(3)解:∠A不可能等于45°.
原因:设∠A=45°,则∠ABC=45°,∠BCP=45°,
∴CP∥AB,与题干中PC与AB交于点P矛盾,
∴∠A不可能等于45°.
【解析】本题主要考查了弦切角的性质,解决问题的关键是根据弦切角的性质结合所给几何条件分析计算即可解决问题,有一定难度.


科目:高中数学 来源: 题型:
【题目】高中流行这样一句话“文科就怕数学不好,理科就怕英语不好”.下表是一次针对高三文科学生的调查所得的数据,试问:在出错概率不超过0.01的前提下文科学生总成绩不好与数学成绩不好有关系吗?
总成绩好 | 总成绩不好 | 总计 | |
数学成绩好 | 20 | 10 | 30 |
数学成绩不好 | 5 | 15 | 20 |
总计 | 25 | 25 | 50 |
(P(K2≥3.841)≈0.05,P(K2≥6.635)≈0.01)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 若f(x1)=f(x2),且x1<x2,关于下列命题:(1)f(x1)>f(﹣x2);(2)f(x2)>f(﹣x1);(3)f(x1)>f(﹣x1);(4)f(x2)>f(﹣x2).正确的个数为( )
若f(x1)=f(x2),且x1<x2,关于下列命题:(1)f(x1)>f(﹣x2);(2)f(x2)>f(﹣x1);(3)f(x1)>f(﹣x1);(4)f(x2)>f(﹣x2).正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知海岛A到海岸公路BC的距离AB=50km,B,C间的距离为100km,从A到C必须先坐船到BC上的某一点D,航速为25km/h,再乘汽车到C,车速为50km/h,记∠BDA=θ
(1)试将由A到C所用的时间t表示为θ的函数t(θ);
(2)问θ为多少时,由A到C所用的时间t最少?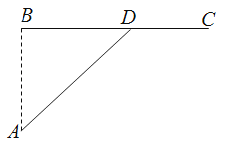
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】轴截面是边长为4 ![]() 的等边三角形的圆锥的直观图如图所示,过底面圆周上任一点作一平面α,且α与底面所成的二面角为
的等边三角形的圆锥的直观图如图所示,过底面圆周上任一点作一平面α,且α与底面所成的二面角为 ![]() ,已知α与圆锥侧面交线的曲线为椭圆,则此椭圆的离心率为( )
,已知α与圆锥侧面交线的曲线为椭圆,则此椭圆的离心率为( ) 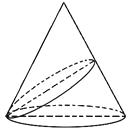
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com