
设函数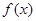 的定义域为
的定义域为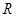 ,对任意的实数
,对任意的实数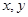 都有
都有 ;当
;当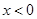 时,
时,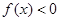 ,且
,且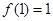 .(1)判断并证明
.(1)判断并证明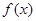 在
在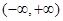 上的单调性;
上的单调性;
(2)若数列 满足:
满足: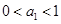 ,且
,且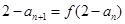 ,证明:对任意的
,证明:对任意的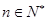 ,
,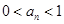
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
设函数![]() 的定义域为R,若存在常数
的定义域为R,若存在常数![]() ,使
,使![]() 对一切实数
对一切实数![]() 均成立,则称
均成立,则称![]() 为“倍约束函数”.现给出下列函数:①
为“倍约束函数”.现给出下列函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 是定义在实数集R上的奇函数,且对一切
是定义在实数集R上的奇函数,且对一切![]() ,
,![]() 均有
均有![]() .其中是“倍约束函数”的序号是
.其中是“倍约束函数”的序号是
查看答案和解析>>
科目:高中数学 来源:2011年辽宁省瓦房店市五校高二上学期竞赛数学理卷 题型:解答题
.(本小题满分12分)设函数 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意实数
,且对任意实数 ,都有
,都有 成立,数列
成立,数列 满足
满足 且
且
(1)求 的值;
的值;
(2)若不等式 对一切
对一切 均成立,求
均成立,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2011年辽宁省瓦房店市五校高二上学期竞赛数学理卷 题型:解答题
.(本小题满分12分)设函数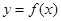 的定义域为R,当
的定义域为R,当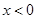 时,
时, ,且对任意实数
,且对任意实数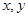 ,都有
,都有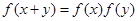 成立,数列
成立,数列 满足
满足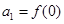 且
且
(1)求 的值;
的值;
(2)若不等式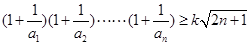 对一切
对一切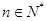 均成立,求
均成立,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2010年江西省高三上学期开学模拟考试理科数学卷 题型:解答题
设函数的定义域为(0,+∞),且对任意正实数x,y都有f(x·y)=f(x)+f(y)恒成立,已知f(2)=1且x>1时f(x)>0.
(1)求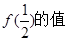 ;
;
(2)判断y=f(x)在(0,+ ∞)上的单调性;
(3)一个各项均为正数的数列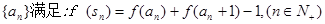 其中sn是数列
其中sn是数列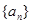 的前n项和,求
的前n项和,求
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com