已知数列{an}的通项公式为an=6n-4,数列{bn}的通项公式为bn=2n,则在数列{an}的前100项中与数列{bn}中相同的项有( )
A.50项
B.34项
C.6项
D.5项
【答案】
分析:{a
n}的前100项中,a
1=6×1-4=2,a
100=6×100-4=596,在598之内,有2
9=512最大.由此进行分类讨论,能求出在数列{a
n}的前100项中与数列{b
n}中相同的项的个数.
解答:解:{a
n}的前100项中,a
1=6×1-4=2,
a
100=6×100-4=596,
在598之内,有2
9=512最大.
∵b
1=2=a
1,
b
2=4,
∵6n-4=4,n=

∉N
*,
∴b
2不是{a
n}中的项;

,
∵6n-4=8,n=2,
∴b
3=a
2;

,
∵6n-4=16,
∴
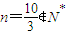
,
∴b
4不是{a
n}中的项;

,
6n-4=32,n=6,
∴b
5=a
6;

,
∵6n-4=64,
∴

,
∴b
6不是{a
n}中的项;

,
6n-4=128,n=22,
∴b
7=a
22;

,
∵6n-4=256,
∴

,
∴b
8不是{a
n}中的项;

,
6n-4=512,n=86,
∴b
9=a
86.
所以在数列{a
n}的前100项中与数列{b
n}中相同的项有5项.
故选D.
点评:本题首先考查等差数列、等比数列的基本量、通项,结合含两个变量的不等式的处理问题,对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.

 ∉N*,
∉N*, ,
, ,
,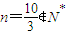 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,

 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案