
已知函数 .
.
(1)求函数 .的单调区间;
.的单调区间;
(2)设函数 的极值.
的极值.
(1) 函数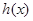 的单调增区间为
的单调增区间为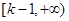 ,单调减区间为
,单调减区间为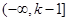
(2) 当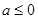 时,
时,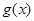 无极值;当
无极值;当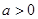 ,
,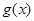 在
在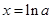 处取得极小值
处取得极小值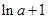 ,无极大值。
,无极大值。
解析试题分析:(1) 求单调区间只需解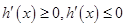 不等式即可;
不等式即可;
(2) 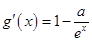 ,在求极值时要对参数
,在求极值时要对参数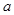 讨论,显然当
讨论,显然当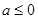 时
时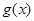 为增函数,无极值,当
为增函数,无极值,当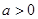 时可求得
时可求得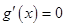 的根,再讨论两侧的单调性;判断极值的方法是先求得
的根,再讨论两侧的单调性;判断极值的方法是先求得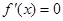 的根,再看在每个根的两侧导函数的正负是否一致,只有两侧导函数的符号不一样才能确定这个根是极值点.这个判断过程通常要放在一个表格中去体现.
的根,再看在每个根的两侧导函数的正负是否一致,只有两侧导函数的符号不一样才能确定这个根是极值点.这个判断过程通常要放在一个表格中去体现.
试题解析:(1) 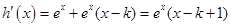
当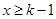 时,
时, 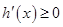 ,
,
当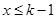 时,
时, 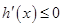 ,
,
故函数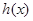 的单调增区间为
的单调增区间为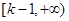 ,单调减区间为
,单调减区间为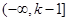 .
.
(2) 由题意: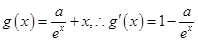
①当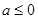 时,
时,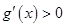 ,
,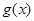 为
为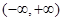 上的增函数,所以
上的增函数,所以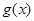 无极值。
无极值。
②当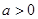 时,令
时,令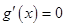 得,
得,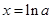
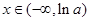 ,
,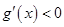 ;
;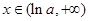 ,
,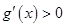
所以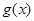 在
在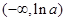 上单调递减,在
上单调递减,在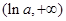 上单调递增
上单调递增
所以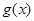 在
在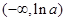 处取得极小值,且极小值为
处取得极小值,且极小值为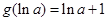 ,无极大值
,无极大值
综上,当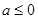 时,
时,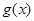 无极值;当
无极值;当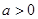 ,
,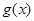 在
在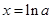 处取得极小值
处取得极小值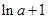 ,无极大值。
,无极大值。
考点:1、函数的单调区间;2、函数的极值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
某地政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知 其中AF是以A为顶点、AD为对称轴的抛物线段.试求该高科技工业园区的最大面积.
其中AF是以A为顶点、AD为对称轴的抛物线段.试求该高科技工业园区的最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数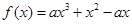 ,其中
,其中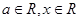 .
.
(1)当 时,求函数
时,求函数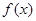 在
在 处的切线方程;
处的切线方程;
(2)若函数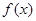 在区间(1,2)上不是单调函数,试求
在区间(1,2)上不是单调函数,试求 的取值范围;
的取值范围;
(3)已知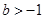 ,如果存在
,如果存在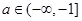 ,使得函数
,使得函数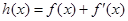
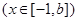 在
在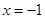 处取得最小值,试求
处取得最小值,试求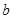 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校操场边有一条小沟,沟沿是两条长150米的平行线段,沟宽 为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为
为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为 ,对称轴与地面垂直,沟深2米,沟中水深1米.
,对称轴与地面垂直,沟深2米,沟中水深1米.
(Ⅰ)求水面宽;
(Ⅱ)如图1所示形状的几何体称为柱体,已知柱体的体积为底面积乘以高,求沟中的水有多少立方米?
(Ⅲ)现在学校要把这条水沟改挖(不准填土)成截面为等腰梯形的沟,使沟的底面与地面平行,沟深不变,两腰分别与抛物线相切(如图2),问改挖后的沟底宽为多少米时,所挖的土最少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,
, .
.
(1)若 ,则
,则 ,
, 满足什么条件时,曲线
满足什么条件时,曲线 与
与 在
在 处总有相同的切线?
处总有相同的切线?
(2)当 时,求函数
时,求函数 的单调减区间;
的单调减区间;
(3)当 时,若
时,若 对任意的
对任意的 恒成立,求
恒成立,求 的取值的集合.
的取值的集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com