
分析 求解得出x=$\frac{3m+3}{m-3}$,分别求解不等式$\frac{3m+3}{m-3}$>0,$\frac{3m+3}{m-3}$<0,f(x)=(m-3)x-3m-3,$\left\{\begin{array}{l}{f(1)•f(2)≤0}\\{f(2)≠0}\end{array}\right.$即$\left\{\begin{array}{l}{(2m+6)(m+9)≤0}\\{-m-9≠0}\end{array}\right.$
求解得出相应的m的范围.
解答 解:∵m(x-3)=3(x+1)
∴(m-3)x=3m+3,
当m≠3时,x=$\frac{3m+3}{m-3}$,
(1)∵$\frac{3m+3}{m-3}$>0,即m>3或m<-1,
∴当m>3或m<-1时,m(x-3)=3(x+1)的解为正数.
(2)∵$\frac{3m+3}{m-3}$<0,即-1<m<3,
∴当-1<m<3时,m(x-3)=3(x+1)的解为负数.
(3)令f(x)=(m-3)x-3m-3,
∵f(1)=-2m-6,
f(2)=-m-9,
$\left\{\begin{array}{l}{f(1)•f(2)≤0}\\{f(2)≠0}\end{array}\right.$
即$\left\{\begin{array}{l}{(2m+6)(m+9)≤0}\\{-m-9≠0}\end{array}\right.$
求解得出:-9<m≤-3
∴当-9<m≤-3时,方程的根在[1,2)内.
点评 本题考查了函数的零点,方程的根,不等式的求解问题,属于简单的综合题目,关键是确定不等式,求解即可.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
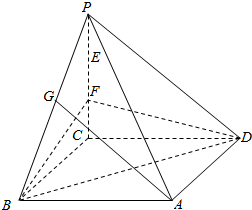 如图,在四棱锥P-ABCD中,已知底面ABCD是平行四边形,E、F是PC的三等分点,G是PB的中点,过E,A,G三点的平面?FBD是否平行?
如图,在四棱锥P-ABCD中,已知底面ABCD是平行四边形,E、F是PC的三等分点,G是PB的中点,过E,A,G三点的平面?FBD是否平行?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
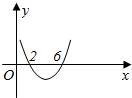 已知函数f(x)=ax(x-c)2在点x=x0处取得极大值32,其导函数y=f′(x)的图象经过点(2,0)、(6,0),如图.
已知函数f(x)=ax(x-c)2在点x=x0处取得极大值32,其导函数y=f′(x)的图象经过点(2,0)、(6,0),如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (-1,1) | C. | [-1,+∞) | D. | [-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 函数f(x)的图象是如图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0),定义函数g(x)=f(x)(1-x).
函数f(x)的图象是如图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0),定义函数g(x)=f(x)(1-x).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com