
设a为实数,设函数![]() 的最大值为g(a)。
的最大值为g(a)。
(Ⅰ)设t=![]() ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)
(Ⅱ)求g(a)
(Ⅲ)试求满足![]() 的所有实数a
的所有实数a
(Ⅰ)![]()
要使有![]() 意义,必须
意义,必须![]() 且
且![]() ,即
,即![]() ,
,
∴![]()
![]() ①
①
![]() 的取值范围是
的取值范围是![]() 由①得
由①得![]()
∴![]()
(Ⅱ)由题意知g(a)即为函数![]() 的最大值。
的最大值。
注意到直线![]() 是抛物线
是抛物线![]() 的对称轴,分以下几种情况讨论。
的对称轴,分以下几种情况讨论。
(1)当![]() 时,函数
时,函数![]()
![]() ,
,![]() 的图象是开口向上的抛物线的一段,由
的图象是开口向上的抛物线的一段,由![]() 知
知![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]()
(2)当![]() 时,
时,![]() ,
, ![]() ,∴
,∴![]() .
.
(3)当![]() 时,函数
时,函数![]() ,
, ![]() 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
若![]() ,即
,即![]() 则
则![]()
若![]() ,即
,即![]() 则
则![]()
若![]() ,即
,即![]() 则
则![]()
综上有 
(Ⅲ)解法一:
情形1:当![]() 时
时![]() ,此时
,此时![]() ,
,![]()
由![]() 解得
解得![]() ,与
,与![]() 矛盾。
矛盾。
情形2:当![]()
![]() 时,此时
时,此时![]() ,
,![]()
![]() 解得,
解得,![]() 与
与![]() 矛盾。
矛盾。
情形3:当![]()
![]() 时,此时
时,此时![]()
所以![]()
情形4:当![]() 时,
时,![]() ,此时
,此时![]() ,
,
![]() ,解得
,解得![]() 与
与![]() 矛盾。
矛盾。
情形5:当![]() 时,
时,![]() ,此时
,此时![]()
![]()
由![]() 解得
解得![]() ,与
,与![]() 矛盾。
矛盾。
情形6:当![]() 时,
时,![]() ,此时
,此时![]() ,
, ![]()
由![]() 解得
解得![]() ,由
,由![]() 得
得![]() .
.
综上知,满足![]() 的所有实数
的所有实数![]() 为
为![]() 或
或![]()


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源:2009-2010学年湖南省长沙市同升湖实验学校高三(上)第二次月考数学试卷(理科)(解析版) 题型:解答题
 的最大值为g(a).
的最大值为g(a). ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t) 的所有实数a
的所有实数a查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省无锡市江阴一中高一(上)第12周数学限时作业(解析版) 题型:解答题
 的最大值为g(a).
的最大值为g(a). ,求t的取值范围,并把f(x)表示为t的函数m(t);
,求t的取值范围,并把f(x)表示为t的函数m(t);查看答案和解析>>
科目:高中数学 来源:2011年北京一零一中学高一上学期期末考试数学卷 题型:解答题
设a为实数,设函数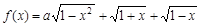 的最大值为g(a)。
的最大值为g(a)。
(Ⅰ)设t= ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)
(Ⅱ)求g(a)
(Ⅲ)试求满足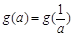 的所有实数a
的所有实数a
查看答案和解析>>
科目:高中数学 来源:2013届江西省上饶市、德兴一中等高二四校联考数学试卷 题型:解答题
设a为实数,设函数 的最大值为g(a)。
的最大值为g(a)。
(Ⅰ)设t=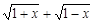 ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)
(Ⅱ)求g(a)(Ⅲ)试求满足 的所有实数a
的所有实数a
查看答案和解析>>
科目:高中数学 来源:江苏高考真题 题型:解答题
 的最大值为g(a)。
的最大值为g(a)。 ,求t的取值范围,并把f(x)表示为t的函数m(t);
,求t的取值范围,并把f(x)表示为t的函数m(t);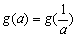 的所有实数a。
的所有实数a。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com