
【题目】记无穷数列![]() 的前n项中最大值为
的前n项中最大值为![]() ,最小值为
,最小值为![]() ,令
,令![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() .
.
(1)若数列![]() 是首项为2,公比为2的等比数列,求
是首项为2,公比为2的等比数列,求![]() ;
;
(2)若数列![]() 是等差数列,试问数列
是等差数列,试问数列![]() 是否也一定是等差数列?若是,请证明;若不是,请举例说明;
是否也一定是等差数列?若是,请证明;若不是,请举例说明;
(3)若![]() ,求
,求![]() .
.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() ,
,![]()
【解析】
(1)由题意求得![]() 和
和![]() ,即得
,即得![]() ,利用等比数列求和公式可得结果.
,利用等比数列求和公式可得结果.
(2)若“数列{bn}是等差数列”,设其公差为d′,bn+1﹣bn![]() d′,根据定义,Mn+1≥Mn,mn+1≤mn,至少有一个取等号,当d′>0时,Mn+1>Mn,an+1=Mn+1>Mn≥an,即数列{an}为增数列,则Mn=an,mn=a1,进而得出.同理可得d′<0时,“数列{an}是等差数列”;当d′=0时,Mn+1=Mn,且mn+1=mn,故{an}为常数列,是等差数列.
d′,根据定义,Mn+1≥Mn,mn+1≤mn,至少有一个取等号,当d′>0时,Mn+1>Mn,an+1=Mn+1>Mn≥an,即数列{an}为增数列,则Mn=an,mn=a1,进而得出.同理可得d′<0时,“数列{an}是等差数列”;当d′=0时,Mn+1=Mn,且mn+1=mn,故{an}为常数列,是等差数列.
(3)由题意可得![]() ,根据定义可以分析得到当
,根据定义可以分析得到当![]() 时,
时,![]() ,即得
,即得![]() ;同理可得
;同理可得![]() 时,
时,![]() .,
.,
所以当![]() 时,
时,![]() ,
,![]() 得到
得到![]() 可得
可得![]() ,求得
,求得
![]() ;当
;当![]() 时,
时,![]() 得到
得到![]() ,求得
,求得![]() ,分段写出结果即可.
,分段写出结果即可.
(1)∵数列![]() 是首项为2,公比为2的等比数列,∴
是首项为2,公比为2的等比数列,∴![]() ,∴
,∴![]() ,
,![]()
则![]() ,∴
,∴![]()
(2)若数列![]() 是等差数列,设其公差为
是等差数列,设其公差为![]()
∵![]()
![]()
根据![]() ,
,![]() 的定义,有以下结论:
的定义,有以下结论:
![]() ,
,![]() ,且两个不等式中至少有一个取等号,
,且两个不等式中至少有一个取等号,
①若![]() ,则必有
,则必有![]() ,∴
,∴![]() ,即对
,即对![]() ,
,![]() ,都有
,都有![]()
∴![]() ,
,![]() ,
,![]()
![]()
∴![]() ,即
,即![]() 为等差数列;
为等差数列;
②当![]() 时,则必有
时,则必有![]() ,所以
,所以![]() ,即对
,即对![]() ,
,![]() ,都有
,都有![]()
∴![]() ,
,![]() ,
,![]()
![]()
所以![]() ,即
,即![]() 为等差数列;
为等差数列;
③当![]() ,
,![]()
![]()
∵![]() ,
,![]() 中必有一个为0,∴根据上式,一个为0,则另一个亦为0,
中必有一个为0,∴根据上式,一个为0,则另一个亦为0,
即![]() ,
,![]() ,∴
,∴![]() 为常数数列,所以
为常数数列,所以![]() 为等差数列,
为等差数列,
综上,数列![]() 也一定是等差数列.
也一定是等差数列.
(3)∵![]() ,
,
∴当![]() 时,
时,![]() ,即
,即![]() ,当
,当![]() 时,
时,![]() ,即
,即![]() .
.
以下证明:![]() ,
,![]()
当![]() 时,
时,
若![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,不合题意;
,不合题意;
若![]() ,则
,则![]() ,
,![]() ,则
,则![]() ,得:
,得:![]() ,与
,与![]() 矛盾,不合题意;
矛盾,不合题意;
∴![]() ,即
,即![]() ;
;
同理可证:![]() ,即
,即![]() ,
,![]() 时,
时,![]() .
.
①当![]() 时,
时,![]() ,
,![]() ∴
∴![]() ∴
∴![]() ,
,![]()
∵![]() ∴
∴![]()
∴![]()
![]()
②当![]() 时,
时,![]() ,且
,且![]()
∴![]() ,则
,则![]() 为
为![]() 或
或![]() .若
.若![]() 为
为![]() ,则
,则![]() 为常数,与题意不符,∴
为常数,与题意不符,∴![]() ∴
∴![]() ∴
∴![]()
∴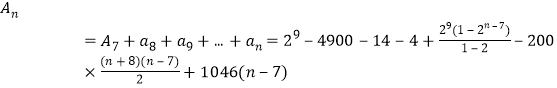
![]() ,
,
∴![]() ,
,![]() .
.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若幂函数![]() 的图象过点
的图象过点![]() ,则
,则![]()
B.命题![]() :“
:“![]() ,
,![]() ”,则
”,则![]() 的否定为“
的否定为“![]() ,
,![]() ”
”
C.“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
D.若![]() 与
与![]() 是相互独立事件,则
是相互独立事件,则![]() 与
与![]() 也是相互独立事件
也是相互独立事件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了美化环境,某公园欲将一块空地规划建成休闲草坪,休闲草坪的形状为如图所示的四边形ABCD.其中AB=3百米,AD=![]() 百米,且△BCD是以D为直角顶点的等腰直角三角形.拟修建两条小路AC,BD(路的宽度忽略不计),设∠BAD=
百米,且△BCD是以D为直角顶点的等腰直角三角形.拟修建两条小路AC,BD(路的宽度忽略不计),设∠BAD=![]() ,
,![]() (
(![]() ,
,![]() ).
).
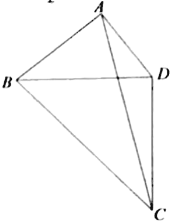
(1)当cos![]() =
=![]() 时,求小路AC的长度;
时,求小路AC的长度;
(2)当草坪ABCD的面积最大时,求此时小路BD的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了丰富学生的课外文化生活,某中学积极探索开展课外文体活动的新途径及新形式,取得了良好的效果.为了调查学生的学习积极性与参加文体活动是否有关,学校对300名学生做了问卷调查,列联表如下:
参加文体活动 | 不参加文体活动 | 合计 | |
学习积极性高 | 180 | ||
学习积极性不高 | 60 | ||
合计 | 300 |
已知在全部300人中随机抽取1人,抽到学习积极性不高的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有![]() 的把握认为学习积极性高与参加文体活动有关?请说明你的理由;
的把握认为学习积极性高与参加文体活动有关?请说明你的理由;
(3)若从不参加文体活动的同学中按照分层抽样的方法选取5人,再从所选出的5人中随机选取2人,求至少有1人学习积极性不高的概率.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中药种植基地有两处种植区的药材需在下周一、下周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘.由于下雨会影响药材品质,基地收益如下表所示:
周一 | 无雨 | 无雨 | 有雨 | 有雨 |
周二 | 无雨 | 有雨 | 无雨 | 有雨 |
收益 |
|
|
|
|
若基地额外聘请工人,可在周一当天完成全部采摘任务.无雨时收益为![]() 万元;有雨时,收益为
万元;有雨时,收益为![]() 万元.额外聘请工人的成本为
万元.额外聘请工人的成本为![]() 万元.
万元.
已知下周一和下周二有雨的概率相同,两天是否下雨互不影响,基地收益为![]() 万元的概率为
万元的概率为![]() .
.
(Ⅰ)若不额外聘请工人,写出基地收益![]() 的分布列及基地的预期收益;
的分布列及基地的预期收益;
(Ⅱ)该基地是否应该外聘工人,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京市政府为做好![]() 会议接待服务工作,对可能遭受污染的某海产品在进入餐饮区前必须进行两轮检测,只有两轮都合格才能进行销售,否则不能销售.已知该海产品第一轮检测不合格的概率为
会议接待服务工作,对可能遭受污染的某海产品在进入餐饮区前必须进行两轮检测,只有两轮都合格才能进行销售,否则不能销售.已知该海产品第一轮检测不合格的概率为![]() ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为![]() ,两轮检测是否合格相互没有影响.
,两轮检测是否合格相互没有影响.
(1)求该海产品不能销售的概率.
(2)如果该海产品可以销售,则每件产品可获利40元;如果该海产品不能销售,则每件产品亏损80元(即获利-80元).已知一箱中有该海产品4件,记一箱该海产品获利![]() 元,求
元,求![]() 的分布列,并求出数学期望
的分布列,并求出数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com