
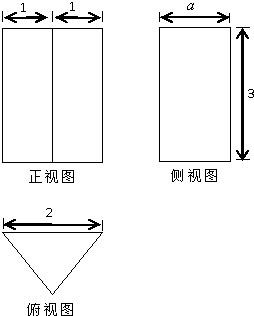
 (1)如图,是一个几何体的三视图,若它的体积是3
(1)如图,是一个几何体的三视图,若它的体积是3| 3 |
科目:高中数学 来源: 题型:
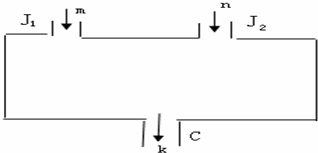 21、如图所示,一个计算装置示意图.J1、J2是数据入口,C 是计算结果的出口.计算过程是:由J1、J2 分别输入自然数m和n,经过计算所得结果由出口C输出k,即:f(m,n)=k.此种计算装置满足以下三个性质:①f(1,1)=1;②f(m,n+1)=f(m,n)+2;③f(m+1,1)=2f(m,1).
21、如图所示,一个计算装置示意图.J1、J2是数据入口,C 是计算结果的出口.计算过程是:由J1、J2 分别输入自然数m和n,经过计算所得结果由出口C输出k,即:f(m,n)=k.此种计算装置满足以下三个性质:①f(1,1)=1;②f(m,n+1)=f(m,n)+2;③f(m+1,1)=2f(m,1).查看答案和解析>>
科目:高中数学 来源: 题型:
 如图是一个方形迷宫,甲、乙两人分别位于迷宫的A、B两处,两人同时以每一分钟一格的速度向东、西、南、北四个方向行走,已知甲向东、西行走的概率都为
如图是一个方形迷宫,甲、乙两人分别位于迷宫的A、B两处,两人同时以每一分钟一格的速度向东、西、南、北四个方向行走,已知甲向东、西行走的概率都为| 1 |
| 4 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
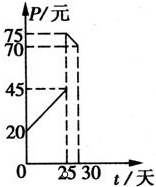 某种商品在30天内每件的销售价格P(元)与时间t(t∈N*)(天)的函数关系用如图的两条线段表示,该商品在30天内日销售量Q(件)与时间t(t∈N*)(天)之间的关系如下表:
某种商品在30天内每件的销售价格P(元)与时间t(t∈N*)(天)的函数关系用如图的两条线段表示,该商品在30天内日销售量Q(件)与时间t(t∈N*)(天)之间的关系如下表:| 第1天 | 5 | 15 | 20 | 30 |
| Q件 | 35 | 25 | 20 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2009•中山模拟)如图,设平面α∩β=EF,AB⊥α,CD⊥α,垂足.分别为B,D,若增加一个条件,就能推出BD⊥EF.现有①AC⊥β;②AC与α,β所成的角相等;③AC与CD在β内的射影在同一条直线上;④AC∥EF.那么上述几个条件中能成为增加条件的个数是( )
(2009•中山模拟)如图,设平面α∩β=EF,AB⊥α,CD⊥α,垂足.分别为B,D,若增加一个条件,就能推出BD⊥EF.现有①AC⊥β;②AC与α,β所成的角相等;③AC与CD在β内的射影在同一条直线上;④AC∥EF.那么上述几个条件中能成为增加条件的个数是( )查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com