
【题目】有下列四个命题:
①“若a2+b2=0,则a,b全为0”的逆否命题是“若a,b全不为0,则a2+b2≠0”
②若事件A与事件B互斥,则P(A∪B)=P(A)+P(B);
③在△ABC中,“A<B”是“sinA<sinB”成立的充要条件;
④若α、β是两个相交平面,直线mα,则在平面β内,一定存在与直线m平行的直线.
上述命题中,其中真命题的序号是_____.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,两焦点与短轴的一个端点的连线构成的三角形面积为
,两焦点与短轴的一个端点的连线构成的三角形面积为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(II)设与圆![]() 相切的直线
相切的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点(
两点(![]() 为坐标原点),
为坐标原点),![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C所对的边分别为a,b,c,bsinA=![]() cosB.
cosB.
(1)求角B的大小;
(2)若b=2,△ABC的面积为![]() ,求a,c.
,求a,c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆![]() 1的左右焦点分别为F1、F2,过焦点F1的直线交椭圆于A、B两点,若△ABF2的内切圆的面积为4,设A、B两点的坐标分别为A(x1,y1),B(x2,y2),则|y1﹣y2|值为_____.
1的左右焦点分别为F1、F2,过焦点F1的直线交椭圆于A、B两点,若△ABF2的内切圆的面积为4,设A、B两点的坐标分别为A(x1,y1),B(x2,y2),则|y1﹣y2|值为_____.
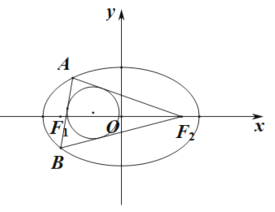
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查民众对国家实行“新农村建设”政策的态度,现通过网络问卷随机调查了年龄在20周岁至80周岁的100人,他们年龄频数分布和支持“新农村建设”人数如下表:

(1)根据上述统计数据填下面的2×2列联表,并判断是否有95%的把握认为以50岁为分界点对“新农村建设”政策的支持度有差异;
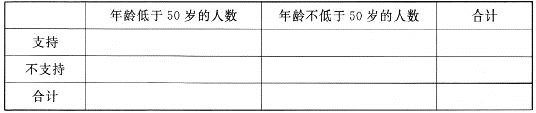
(2)现从年龄在[70,80]内的5名被调查人中任选两人去参加座谈会,求选出两人中恰有一人支持新农村建设的概率.
参考数据:

参考公式:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点在平面直角坐标系的原点![]() 处,极轴与
处,极轴与![]() 轴的非负半轴重合,且长度单位相同,直线
轴的非负半轴重合,且长度单位相同,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() (
(![]() 为参数).其中
为参数).其中![]() .
.
(1)试写出直线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 的普通方程;
的普通方程;
(2)若点![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到直线
到直线![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他们各应偿还多少?已知牛、马、羊的主人各应偿还![]() 升,
升, ![]() 升,
升, ![]() 升,1斗为10升,则下列判断正确的是( )
升,1斗为10升,则下列判断正确的是( )
A. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
B. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
C. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
D. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com