
【题目】如图所示的多面体中, AC⊥BC,四边形ABED是正方形,平面ABED⊥平面ABC,点F,G,H分别为BD,EC,BE的中点,求证:
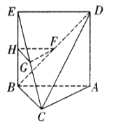
(1) BC⊥平面ACD
(2)平面HGF∥平面ABC.
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点
的焦点![]() 的直线与抛物线在第一象限的交点为
的直线与抛物线在第一象限的交点为![]() ,与抛物线准线的交点为
,与抛物线准线的交点为 ![]() ,点
,点![]() 在抛物线准线上的射影为
在抛物线准线上的射影为![]() ,若
,若![]() 的面积为
的面积为![]() .
.
( 1 ) 求抛物线的标准方程;
( 2 ) 过焦点![]() 的直线与抛物线交于
的直线与抛物线交于![]() 两点,抛物线在
两点,抛物线在![]() 点处的切线分别为
点处的切线分别为![]() ,且
,且![]() 与
与![]() 相交于
相交于![]() 点,
点,![]() 与
与![]() 轴交于
轴交于![]() 点,求证:
点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】羽毛球比赛中采用每球得分制,即每回合中胜方得1分,负方得0分,每回合由上回合的胜方发球.设在甲、乙的比赛中,每回合发球,发球方得1分的概率为0.6,各回合发球的胜负结果相互独立.若在一局比赛中,甲先发球.
(1)求比赛进行3个回合后,甲与乙的比分为![]() 的概率;
的概率;
(2)![]() 表示3个回合后乙的得分,求
表示3个回合后乙的得分,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】寒假即将到来,某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每在支出20元的各种费用(人工费,消耗费用等等).受市场调控,每个房间每天的房价不得高于340元.设每个房间的房价每天增加x元(x为10的正整数倍)
(1)设宾馆一天的利润为W元, 求W与x的函数关系式;
(2)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数![]() 满足:对任意
满足:对任意![]() 都有
都有![]() .
.
(1)求证:函数![]() 是奇函数;
是奇函数;
(2)如果当![]() 时,有
时,有![]() ,试判断
,试判断![]() 在
在![]() 上的单调性,并用定义证明你的判断;
上的单调性,并用定义证明你的判断;
(3)在(2)的条件下,若![]() 对满足不等式
对满足不等式![]() 的任意
的任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在无穷数列![]() 中,
中,![]() ,对于任意
,对于任意![]() ,都有
,都有![]() ,
,![]() ,设
,设![]() ,记使得
,记使得![]() 成立的
成立的![]() 的最大值为
的最大值为![]() .
.
(![]() )设数列
)设数列![]() 为
为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,写出
,写出![]() ,
,![]() ,
,![]() 的值.
的值.
(![]() )若
)若![]() 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列![]() .
.
(![]() )设
)设![]() ,
,![]() ,求
,求![]() 的值.(用
的值.(用![]() ,
,![]() ,
,![]() 表示)
表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某餐厅经营盒饭生意,每天的房租、人员工资等固定成本为200元,每盒盒饭的成本为15元,销售单价与日均销售量的关系如下表

根据以上数据,当这个餐厅每盒盒饭定价______元时,利润最大
A.16.5B.19.5C.21.5D.22
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com