
【题目】在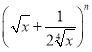 的展开式中,前3项的系数成等差数列,
的展开式中,前3项的系数成等差数列,
(1)求![]() 的值;
的值;
(2)求展开式中二项式系数最大的项及各项系数和;
(3)求展开式中含![]() 的项的系数及有理项.
的项的系数及有理项.
【答案】(1)![]() (2)最大的项为第五项,
(2)最大的项为第五项,![]() ;
;![]() (3)
(3)![]() ;
;![]() ;
;![]() ;
;![]() .
.
【解析】
(1)根据前3项的系数成等差数列,利用等差数列的定义求得![]() 的值;
的值;
(2)根据通项公式、二项式系数的性质求展开式中二项式系数最大的项,令![]() 即可求得展开式系数和;
即可求得展开式系数和;
(3)在二项展开式的通项公式中,令![]() 的幂指数等于
的幂指数等于![]() ,求出
,求出![]() 的值,即可求得含
的值,即可求得含![]() 的项的系数.设展开式中第
的项的系数.设展开式中第![]() 项为有理项,则
项为有理项,则![]() ,当
,当![]() 、4、8时对应的项为有理项.
、4、8时对应的项为有理项.
解:(1)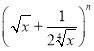 展开式的通项为
展开式的通项为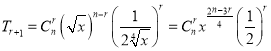
因为前3项的系数成等差数列,且前三项系数为![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() (舍去)或
(舍去)或![]() .
.
(2)因为![]() ,
,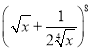 所以展开式中二项式系数最大的项为第五项,
所以展开式中二项式系数最大的项为第五项,
即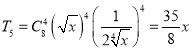 .
.
令![]() 得
得![]() ,即展开式系数和为
,即展开式系数和为![]()
(3)通项公式: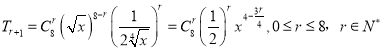
![]()
由![]() ,
,![]() ,
,
可得含![]() 的项的系数为
的项的系数为![]() .
.
设展开式中第![]() 项为有理项,由
项为有理项,由![]()
当![]() 、4、8时对应的项为有理项,有理项分别为:
、4、8时对应的项为有理项,有理项分别为:![]() ;
;![]() ;
;![]() .
.


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
【题目】将杨辉三角中的奇数换成1,偶数换成0,便可以得到如图的“0-1三角”.在“![]() 三角”中,从第1行起,设第n
三角”中,从第1行起,设第n![]() 次出现全行为1时,1的个数为
次出现全行为1时,1的个数为![]() ,则
,则![]() 等于( )
等于( )

A.13B.14C.15D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为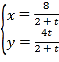 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() (
(![]() )与直线
)与直线![]() 和曲线
和曲线![]() 分别交于
分别交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市的华为手机专卖店对该市市民使用华为手机的情况进行调查.在使用华为手机的用户中,随机抽取100名,按年龄(单位:岁)进行统计的频率分布直方图如图:

(1)根据频率分布直方图,分别求出样本的平均数(同一组数据用该区间的中点值作代表)和中位数的估计值(均精确到个位);
(2)在抽取的这100名市民中,按年龄进行分层抽样,抽取20人参加华为手机宣传活动,现从这20人中,随机选取2人各赠送一部华为手机,求这2名市民年龄都在![]() 内的人数为
内的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直三棱柱![]() 中的底面为等腰直角三角形,
中的底面为等腰直角三角形,![]() ,点
,点![]() 分别是边
分别是边![]() ,
,![]() 上动点,若直线
上动点,若直线![]() 平面
平面![]() ,点
,点![]() 为线段
为线段![]() 的中点,则
的中点,则![]() 点的轨迹为
点的轨迹为![]()
![]()
A. 双曲线的一支![]() 一部分
一部分![]() B. 圆弧
B. 圆弧![]() 一部分
一部分![]()
C. 线段![]() 去掉一个端点
去掉一个端点![]() D. 抛物线的一部分
D. 抛物线的一部分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】针对“中学生追星问题”,某校团委对“学生性别和中学生追星是否有关”作了一次调查,其中女生人数是男生人数的![]() ,男生追星的人数占男生人数的
,男生追星的人数占男生人数的![]() ,女生追星的人数占女生人数的
,女生追星的人数占女生人数的![]() .若有
.若有![]() 的把握认为是否追星和性别有关,则男生至少有( )
的把握认为是否追星和性别有关,则男生至少有( )
参考数据及公式如下:
|
|
|
|
|
|
|
|
![]()
A. 12B. 11C. 10D. 18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com