【题目】
年初，湖北出现由新型冠状病毒引发的肺炎.各级政府相继启动重大突发公共卫生事件一级响应，全国齐心抗击疫情，基本上控制住了疫情.下图为
月
日至
月
日我国新型冠状病毒肺炎全国总新增确诊人数和新增境外输入确诊人数趋势图(数据来源：国家卫健委官网)，则下列表述中错误的是（ ）
A.3月上旬全国总新增确诊人数呈波动下降趋势.
B.3月中下旬全国总新增确诊人数开始反弹的主要原因是境外输入病例的增加.
C.全国总新增确诊人数随着境外输入确诊人数变化而变化.
D.4月中下旬国内新增确诊人数呈越来越少的趋势.
黄冈冠军课课练系列答案科目：高中数学 来源： 题型：
【题目】已知抛物线
的焦点曲线
的一个焦点， 
为坐标原点，点
为抛物线
上任意一点，过点
作
轴的平行线交抛物线的准线于
，直线
交抛物线于点
.
（Ⅰ）求抛物线
的方程；
（Ⅱ）求证：直线
过定点
，并求出此定点的坐标.
【答案】（I）
；（II）证明见解析.
【解析】试题分析：（Ⅰ）将曲线
化为标准方程，可求得
的焦点坐标分别为
，可得
，所以
，即抛物线的方程为
；（Ⅱ）结合（Ⅰ），可设
，得
，从而直线
的方程为
,联立直线与抛物线方程得
，解得
，直线
的方程为
，整理得
的方程为
，此时直线恒过定点
.
试题解析：（Ⅰ）由曲线
，化为标准方程可得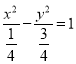
， 所以曲线
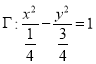是焦点在
轴上的双曲线，其中
，故
， 
的焦点坐标分别为
，因为抛物线的焦点坐标为
，由题意知
，所以
，即抛物线的方程为
.
（Ⅱ）由（Ⅰ）知抛物线
的准线方程为
，设
，显然
.故
，从而直线
的方程为
,联立直线与抛物线方程得
，解得
①当
，即
时，直线
的方程为
，
②当
，即
时，直线
的方程为
，整理得
的方程为
，此时直线恒过定点
， 
也在直线
的方程为
上，故直线
的方程恒过定点
.
【题型】解答题
【结束】
21
【题目】已知函数
， 
（Ⅰ）当
时，求函数
的单调递减区间；
（Ⅱ）若
时，关于
的不等式
恒成立，求实数
的取值范围；
（Ⅲ）若数列
满足
， 
，记
的前
项和为
，求证： 
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某车间甲组有10名工人，其中有4名女工人；乙组有5名工人，其中有3名女工人，现采用分层抽样方法从甲、乙两组中共抽取3名工人进行技术考核.
（1）求从甲、乙两组各抽取的人数；
（2）求从甲组抽取的工人中恰有1名女工人的概率；
（3）记X表示抽取的3名工人中男工人人数，求X的分布列和数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图4所示，其中成绩分组区间是： 
，
，
，
，
.
（1）求图中
的值；
（2）根据频率分布直方图，估计这100名学生语文成绩的平均分；
（3）若这100名学生语文成绩某些分数段的人数
与数学成绩相应分数段的人数
之比如下表所示，求数学成绩在
之外的人数.
分数段 |
|
|
|
|
X:y | 1:1 | 2:1 | 3:4 | 4:5 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】总体由编号为01，02，…，19，20的20个个体组成，利用下面的随机数表选取6个个体，选取方法从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第6个个体的编号为（ ）
7816 6572 0802 6314 0702 4369 9728 0198 |
3204 9234 4935 8200 3623 4869 6938 7481 |
A.07B.04C.02D.01
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某大型超市在2018年元旦举办了一次抽奖活动，抽奖箱里放有3个红球，3个黄球和1个蓝球（这些小球除颜色外大小形状完全相同），从中随机一次性取3个小球，每位顾客每次抽完奖后将球放回抽奖箱.活动另附说明如下：
①凡购物满100（含100）元者，凭购物打印凭条可获得一次抽奖机会；
②凡购物满188（含188）元者，凭购物打印凭条可获得两次抽奖机会；
③若取得的3个小球只有1种颜色，则该顾客中得一等奖，奖金是一个10元的红包；
④若取得的3个小球有3种颜色，则该顾客中得二等奖，奖金是一个5元的红包；
⑤若取得的3个小球只有2种颜色，则该顾客中得三等奖，奖金是一个2元的红包.
抽奖活动的组织者记录了该超市前20位顾客的购物消费数据（单位：元），绘制得到如图所示的茎叶图.
（1）求这20位顾客中奖得抽奖机会的顾客的购物消费数据的中位数与平均数（结果精确到整数部分）；
（2）记一次抽奖获得的红包奖金数（单位：元）为
，求
的分布列及数学期望，并计算这20位顾客（假定每位获得抽奖机会的顾客都会去抽奖）在抽奖中获得红包的总奖金数的平均值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】海中一小岛
的周围
内有暗礁，海轮由西向东航行至
处测得小岛
位于北偏东
，航行8
后，于
处测得小岛
在北偏东
（如图所示）.
（1）如果这艘海轮不改变航向，有没有触礁的危险？请说明理由.
（2）如果有触礁的危险，这艘海轮在
处改变航向为东偏南
（
）方向航行，求
的最小值.
附： 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
