
【题目】已知椭圆![]() 上的点
上的点![]() (不包括横轴上点)满足:与
(不包括横轴上点)满足:与![]() ,
,![]() 两点连线的斜率之积等于
两点连线的斜率之积等于![]() ,
,![]() ,
,![]() 两点也在曲线
两点也在曲线![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的右焦点作斜率为1的直线交椭圆于
的右焦点作斜率为1的直线交椭圆于![]() ,
,![]() 两点,求
两点,求![]() ;
;
(3)求椭圆上的点到直线![]() 距离的最小值.
距离的最小值.
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O。D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形。沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥。当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为_______。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义满足不等式|x![]() A|<B(A∈R,B>0)的实数x的集合叫做A的B邻域.若a+b
A|<B(A∈R,B>0)的实数x的集合叫做A的B邻域.若a+b![]() t(t为正常数)的a+b邻域是一个关于原点对称的区间,则a2+b2的最小值为______.
t(t为正常数)的a+b邻域是一个关于原点对称的区间,则a2+b2的最小值为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() 是边长等于2的等边三角形,四边形
是边长等于2的等边三角形,四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的点,
上的点,![]() .
.![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
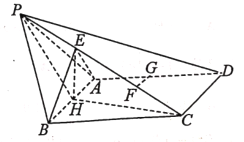
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |

(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年10月9日,教育部考试中心下发了《关于2017年普通高考考试大纲修订内容的通知》,在各科修订内容中明确提出,增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用.宿州市教育部门积极回应,编辑传统文化教材,在全市范围内开设书法课,经典诵读等课程.为了了解市民对开设传统文化课的态度,教育机构随机抽取了200位市民进行了解,发现支持开展的占![]() ,在抽取的男性市民120人中持支持态度的为80人.
,在抽取的男性市民120人中持支持态度的为80人.
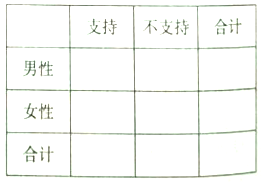
(Ⅰ)完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为性别与支持与否有关?
的把握认为性别与支持与否有关?
(Ⅱ)为了进一步征求对开展传统文化的意见和建议,从抽取的200位市民中对不支持的按照分层抽样的方法抽取5位市民,并从抽取的5人中再随机选取2人进行座谈,求选取的2人恰好为1男1女的概率.
附: 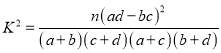 .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com