
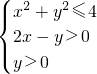 ,则
,则 的最大值为
的最大值为



 =(1,1)•(x,y)=x+y,设z=x+y,再利用z的几何意义求最值,只需求出直线z=x+y过可行域内的点A时,z最大即可.
=(1,1)•(x,y)=x+y,设z=x+y,再利用z的几何意义求最值,只需求出直线z=x+y过可行域内的点A时,z最大即可. 解:先根据约束条件画出可行域,
解:先根据约束条件画出可行域, =(1,1)•(x,y)=x+y,
=(1,1)•(x,y)=x+y, ,
, )时,z最大,
)时,z最大, .
.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
|
| OM |
| ON |
A、
| ||
B、2
| ||
C、
| ||
D、2
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
| OM |
| ON |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| MN |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| OM |
| ON |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省高三高考模拟卷(二)理科数学试卷(解析版) 题型:选择题
设O为坐标原点,点M的坐标为(2,1),若点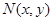 满足不等式组
满足不等式组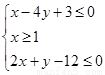 ,则使
,则使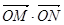 取得最大值的点N有
取得最大值的点N有
A.1个 B.2个 C.3个 D.无数个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com