
分析 ①由正弦定理进行判断,
②根据三角形的边角关系进行判断,
③根据等比数列的性质进行判断,
④根据向量投影的公式进行判断,
⑤根据长方体的体对角线和外接球的直径相等进行求解.
解答  解:①在△ABC中,若sinA>sinB,由正弦定理得a>b,则A>B成立,故①正确,
解:①在△ABC中,若sinA>sinB,由正弦定理得a>b,则A>B成立,故①正确,
②若满足条件C=60°,AB=$\sqrt{3}$,BC=a,则三角形的高AD=h=asinC=$\frac{\sqrt{3}}{2}$a,
若满足条件的△ABC有两个,则$\left\{\begin{array}{l}{\sqrt{3}>\frac{\sqrt{3}}{2}a}\\{\sqrt{3}<a}\end{array}\right.$,即$\left\{\begin{array}{l}{a<2}\\{a>\sqrt{3}}\end{array}\right.$,得$\sqrt{3}$<a<2故②错误,
③在等比数列{an}中,若其前n项和Sn=3n+a,可得a1=3+a,当n≥2时,an=Sn-Sn-1=2•3n-1,a2=6,a3=18,则62=18(3+a),解得a=-1,因此正确;
④若向量$\vec a=(1,1)$,$\vec b=(1,-2)$,则向量$\vec a$在向量$\vec b$方向上的投影为|$\vec a$|cos<$\vec a$,$\vec b$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$=$\frac{1-2}{\sqrt{1+4}}=-\frac{\sqrt{5}}{5}$,故④错误;
⑤空间中长度分别为1,2,3的线段OA、OB、OC两两相互垂直,若四点O、A、B、C在球面上,
则以OA、OB、OC为棱的长方体的体对角线为直径,即2R=$\sqrt{{1}^{2}+{2}^{2}+{3}^{2}}$=$\sqrt{14}$.
则球半径R=$\frac{\sqrt{14}}{2}$,则该球的体积为$\frac{4}{3}•$π($\frac{\sqrt{14}}{2}$)3=$\frac{{7\sqrt{14}}}{3}$π;故⑤正确,
故答案为:①③⑤
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,有一定的难度.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
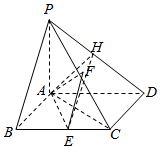 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,E,F分别是BC,PC的中点,H是PD上的动点,EH与平面PAD所成的角为θ.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,E,F分别是BC,PC的中点,H是PD上的动点,EH与平面PAD所成的角为θ.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com