
分析 我们先画出约束条件中不含参数的几个不等式表示的平面区域,根据该平面区域的形状是一个轴对称四边形围成的区域,和含参数的直线所表示的意义,分析满足条件的k的取值.
解答 解:先将不等式前三个不等式所表示的平面区域,
三个顶点分别为O(0,0),A(2$\sqrt{2}$+2,0),(0,2$\sqrt{2}$+2),
x-ky+2k=0,表示的恒过点C(0,2)的直线,
若不等式组表示的是一个对称的四边形区域,
则直线x-ky+2k=0,与直线AB:x+y-2$\sqrt{2}$-2=0,平行或垂直,
即直线x-ky+2k=0的斜率$\frac{1}{k}$=±1,
解得k=±1,
故答案为:±1.
点评 本题主要考查二元一次不等式组表示平面区域的问题,则解题时,关键是正确地画出平面区域,然后结合分类讨论的思想,针对图象分析满足条件的参数的取值范围.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
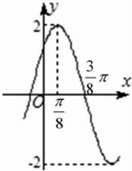 函数f(x)=2sin(ωx+φ),(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,
函数f(x)=2sin(ωx+φ),(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有且只有一个 | B. | 可能有两个 | C. | 至多有一个 | D. | 有两个以上 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com