
|
|
|


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
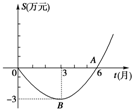 2009年某个体企业受金融危机和国家政策调整的影响,经历了从亏损到盈利的过程,下面的二次函数图象(部分)刻画了该公司年初以来的累积利润S(万元)与时间t(月)之间的关系(即前t个月的利润总和S与t之间的关系,0≤t≤12).请根据图象提供的信息解答下列问题:
2009年某个体企业受金融危机和国家政策调整的影响,经历了从亏损到盈利的过程,下面的二次函数图象(部分)刻画了该公司年初以来的累积利润S(万元)与时间t(月)之间的关系(即前t个月的利润总和S与t之间的关系,0≤t≤12).请根据图象提供的信息解答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:
| Sn•an |
| 8n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| x2+x+1 |
| 1 |
| 5x2-4x+11 |
| 1 |
| 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com