
【题目】将函数h(x)=2sin(2x+ ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位,再向上平移2个单位,得到函数f(x)的图象,则函数f(x)的图象( )
个单位,再向上平移2个单位,得到函数f(x)的图象,则函数f(x)的图象( )
A.关于直线x=0对称
B.关于直线x=π对称
C.关于点( ![]() ,0)对称
,0)对称
D.关于点( ![]() ,2)对称
,2)对称
【答案】D
【解析】解:将函数h(x)=2sin(2x+ ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位,
个单位,
可得y=2sin[2(x﹣ ![]() )+
)+ ![]() ]=2sin(2x﹣
]=2sin(2x﹣ ![]() )的图象;
)的图象;
再向上平移2个单位,得到函数f(x)=2sin(2x﹣ ![]() )+2的图象,
)+2的图象,
∵ ![]() ,
,
∴f(x)的图象关于点 ![]() 对称,
对称,
故选:D.
【考点精析】根据题目的已知条件,利用函数y=Asin(ωx+φ)的图象变换的相关知识可以得到问题的答案,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


科目:高中数学 来源: 题型:
【题目】下列命题中:①、若m>0,则方程x2﹣x+m=0有实根. ②、若x>1,y>1,则x+y>2的逆命题. ③、对任意的x∈{x|﹣2<x<4},|x﹣2|<3的否定形式. ④、△>0是一元二次方程ax2+bx+c=0有一正根和一负根的充要条件.是真命题的有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(1,2),
=(1,2), ![]() =(x,1);
=(x,1);
(1)若( ![]() +2
+2 ![]() )⊥(2
)⊥(2 ![]() ﹣
﹣ ![]() )时,求x的值;
)时,求x的值;
(2)若向量 ![]() 与向量
与向量 ![]() 的夹角为锐角,求x的取值范围.
的夹角为锐角,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017南京一模19】设函数![]() ,
,![]() .
.
(1)当![]() 时,解关于
时,解关于![]() 的方程
的方程![]() (其中
(其中![]() 为自然对数的底数);
为自然对数的底数);
(2)求函数![]() 的单调增区间;
的单调增区间;
(3)当![]() 时,记函数
时,记函数![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式
![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某通讯公司需要在三角形地带OAC区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域BOC内,乙中转站建在区域AOB内.分界线OB固定,且OB=(1+ ![]() )百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°.设OA=x(3≤x≤6)百米,OC=y百米.
)百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°.设OA=x(3≤x≤6)百米,OC=y百米.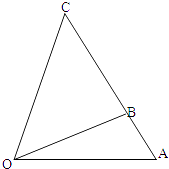
(1)试将y表示成x的函数,并求出函数y的解析式;
(2)当x取何值时?整个中转站的占地面积S△OAC最小,并求出其面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生的身体状况,某校随机抽取了一批学生测量体重.经统计,这批学生的体重数据(单位:千克)全部介于45至70之间.将数据分成以下5组:第1组[45,50),第2组[50,55),第3组[55,60),第4组[60,65),第5组[65,70],得到如图所示的频率分布直方图.现采用分层抽样的方法,从第3,4,5组中随机抽取6名学生做初检.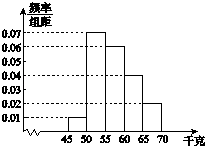
(1)求每组抽取的学生人数;
(2)若从6名学生中再次随机抽取2名学生进行复检,求这2名学生不在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点C(t, ![]() )(t∈R,t≠0)为圆心的圆过原点O.
)(t∈R,t≠0)为圆心的圆过原点O.
(1)设直线3x+y﹣4=0与圆C交于点M、N,若|OM|=|ON|,求圆C的方程;
(2)在(1)的条件下,设B(0,2),且P、Q分别是直线l:x+y+2=0和圆C上的动点,求|PQ|﹣|PB|的最大值及此时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【南京市、盐城市2017届高三年级第二次模拟】(本小题满分14分)
在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,然后在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒(如图).设小正方形边长为x厘米,矩形纸板的两边AB,BC的长分别为a厘米和b厘米,其中a≥b.
(1)当a=90时,求纸盒侧面积的最大值;
(2)试确定a,b,x的值,使得纸盒的体积最大,并求出最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com