练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

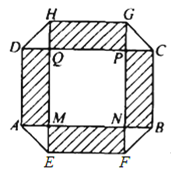
    【题目】如图，居民小区要建一座八边形的休闲场所，它的主体造型平面图是由两个相同的矩形和构成的面积为的十字形地域，计划在正方形上建一座花坛，造价为元/；在四个相同的矩形（图中阴影部分）上铺上花岗岩地坪，造价为元/；再在四个空角（图中四个三角形，如）上铺草坪，造价为元/

    （1）设总造价为（单位：元），长为（单位：），试求出关于的函数关系式，并求出定义域；

    （2）当长取何值时，总造价最小，并求出这个最小值.

    【答案】（1）；（2）

    【解析】

    （1）设，根据十字形地域的面积得出的关系式，并用表示.将花坛、地坪、草坪的造价相加，求得总造价，并求得的取值范围.

    （2）利用基本不等式求得的最小值，并求得此时对应的的值.

    （1）设，则，

    ；

    （2），

    当且仅当，即时，（元）

    答：当，即时，总造价最小.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中， , ，点为棱的中点.

    （1）证明： 平面；

    （2）若，求三棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知与相交于点，线段是圆的一条动弦，且，则的最小值是___________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点，及圆．

    （1）求过点的圆的切线方程；

    （2）若过点的直线与圆相交，截得的弦长为，求直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线C：y2＝2px(p＞0)的焦点F，直线y＝4与y轴的交点为P，与抛物线C的交点为Q，且|QF|＝2|PQ|．

    (1)求p的值；

    (2)已知点T(t，－2)为C上一点，M，N是C上异于点T的两点，且满足直线TM和直线TN的斜率之和为，证明直线MN恒过定点，并求出定点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆过点，其长轴、焦距和短轴的长的平方依次成等差数列直线l与x轴正半轴和y轴分别交于点Q、P，与椭圆分别交于点M、N，各点均不重合且满足．

    求椭圆的标准方程；

    若，试证明：直线l过定点并求此定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，以为极点，轴为正半轴为极轴建立极坐标系.已知曲线的极坐标方程为 ，直线与曲线相交于两点，直线过定点且倾斜角为交曲线于两点.

    （1）把曲线化成直角坐标方程，并求的值；

    （2）若成等比数列，求直线的倾斜角.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C1：y2＝1的左右顶点是双曲线C2：的顶点，且椭圆C1的上顶点到双曲线C2的渐近线的距离为．

    （1）求双曲线C2的方程；

    （2）若直线与C1相交于M1，M2两点，与C2相交于Q1，Q2两点，且5，求|M1M2|的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知四面体ABCD中，DA=DB=DC=且DA、DB、DC两两互相垂直，点是△ABC的中心.

    (1)求直线DA与平面ABC所成角的大小(用反三角函数表示)；

    (2)过作OE⊥AD，垂足为E，求ΔDEO绕直线DO旋转一周所形成的几何体的体积；

    (3)将△DAO绕直线DO旋转一周，则在旋转过程中，直线DA与直线BC所成角记为，求的取值范图.

    查看答案和解析>>

    同步练习册答案