
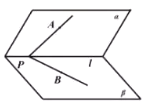
【题目】如图,二面角![]() 中,
中,![]() ,射线
,射线![]() ,
,![]() 分别在平面
分别在平面![]() ,
,![]() 内,点A在平面
内,点A在平面![]() 内的射影恰好是点B,设二面角
内的射影恰好是点B,设二面角![]() 、
、![]() 与平面
与平面![]() 所成角、
所成角、![]() 与平面
与平面![]() 所成角的大小分别为
所成角的大小分别为![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
由题意画出图形,分别找出二面角及线面角,结合正切函数的单调性及平面的斜线与平面内所有直线所成角中的最小角是线面角进行大小比较.
解:当PA⊥l,PB⊥l时,δ=φ=θ;
当PA,PB与l均不垂直时,如图:
由已知AB⊥β,可得AB⊥l,过A作AO⊥l,连接OB,则OB⊥l,
可得∠AOB为δ,∠APB=φ,
在平面AOB内,过B作BI⊥AO,则BI⊥α,连接PI,则∠BPI=θ,
在Rt△ABO与Rt△ABP中,可得tanδ![]() ,tanφ
,tanφ![]() ,由AB=AB,PB>OB,
,由AB=AB,PB>OB,
可得tanδ>tanφ,则δ>φ;
PB为平面α的一条斜线,PB与α内所有直线所成角的最小角为θ,即φ>θ.
∴δ>φ>θ.
综上,δ≥φ≥θ.
故选:A.



 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() (x∈R,实数a∈[0,+∞),e=2.71828…是自然对数的底数,
(x∈R,实数a∈[0,+∞),e=2.71828…是自然对数的底数,![]() ).
).
(Ⅰ)若f(x)≥0在x∈R上恒成立,求实数a的取值范围;
(Ⅱ)若ex≥lnx+m对任意x>0恒成立,求证:实数m的最大值大于2.3.
查看答案和解析>>
科目:高中数学 来源: 题型:
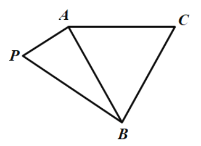
【题目】如图所示,平面四边形![]() 中,
中,![]() 为直角,
为直角,![]() 为等边三角形,现把
为等边三角形,现把![]() 沿着
沿着![]() 折起,使得平面
折起,使得平面![]() 与平面
与平面![]() 垂直,且点M为
垂直,且点M为![]() 的中点.
的中点.
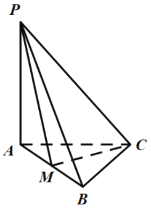
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南北朝时期的数学家祖暅提出了计算几何体体积的祖暅原理:“幂势既同,则积不容异“.意思是两个同高的几何体,如果在等高处的截面积都相等,那么这两个几何体的体积相等.现有某几何体和一个圆锥满足祖暅原理的条件,若该圆锥的侧面展开图是半径为3的圆的三分之一,则该几何体的体积为( )
A.![]() πB.
πB.![]() πC.4
πC.4![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为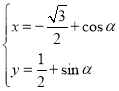 (
(![]() 为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系.
为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系.
(1)设射线l的极坐标方程为![]() ,若射线l与曲线C交于A,B两点,求AB的长;
,若射线l与曲线C交于A,B两点,求AB的长;
(2)设M,N是曲线C上的两点,若∠MON![]() ,求
,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为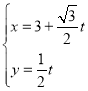 (
(![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点、以
为极点、以![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求线段![]() 的中点
的中点![]() 的直角坐标;
的直角坐标;
(2)设点![]() 是曲线
是曲线![]() 上任意一点,求
上任意一点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 1(a>b>0)的离心率为
1(a>b>0)的离心率为![]() ,点M(a,0),N(0,b),O(0,0),且△OMN的面积为1.
,点M(a,0),N(0,b),O(0,0),且△OMN的面积为1.
(1)求椭圆C的标准方程;
(2)设A,B是x轴上不同的两点,点A(异于坐标原点)在椭圆C内,点B在椭圆C外.若过点B作斜率不为0的直线与C相交于P,Q两点,且满足∠PAB+∠QAB=180°.证明:点A,B的横坐标之积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是2020项的实数数列,
是2020项的实数数列,![]() 中的每一项都不为零,
中的每一项都不为零,![]() 中任意连续11项
中任意连续11项![]() 的乘积是定值
的乘积是定值![]() .
.
①存在满足条件的数列,使得其中恰有365个1;
②不存在满足条件的数列,使得其中恰有550个1.
命题的真假情况为( )
A.①和②都是真命题B.①是真命题,②是假命题
C.②是真命题,①是假命题D.①和②都是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
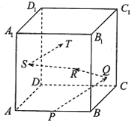
【题目】如图,在正方体![]() 中,棱
中,棱![]() 的中点为
的中点为![]() ,若光线从点
,若光线从点![]() 出发,依次经三个侧面
出发,依次经三个侧面![]() ,
,![]() ,
,![]() 反射后,落到侧面
反射后,落到侧面![]() (不包括边界),则入射光线
(不包括边界),则入射光线![]() 与侧面
与侧面![]() 所成角的正切值的范围是( )
所成角的正切值的范围是( )
A.![]() B.
B.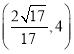 C.
C. D.
D.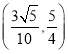
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com