
 |.
|. +
+ +
+ ≤
≤ .
. ,可以求出k值;
,可以求出k值;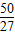 恒成立,可以转化为
恒成立,可以转化为 ≤
≤ (2x-x2),利用此不等式进行放缩,从而进行证明;
(2x-x2),利用此不等式进行放缩,从而进行证明; 得:
得: |x1-x2|=
|x1-x2|=
 =
= =
=
 ,…(6分)
,…(6分)| x | (0, ) ) |  | ( ,1) ,1) | 1 | |
| F′(x) | - | + | |||
| F(x) | 2 | 减函数 |  | 增函数 | 2 |
 )=
)= ; …(10分)
; …(10分) 恒成立,
恒成立, ≤
≤ (2-x),有
(2-x),有 ≤
≤ (2x-x2),…(12分)
(2x-x2),…(12分) +
+ +
+ ≤
≤ [2(sinα+sinβ+sinγ)-(sin2α+sin2β+sin2γ)
[2(sinα+sinβ+sinγ)-(sin2α+sin2β+sin2γ) …(14分)
…(14分) ,
, +
+ +
+ ≤
≤ (2-
(2- )=
)= ,
, 时,等号成立.…(16分)
时,等号成立.…(16分)

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| y |
| f1(x)ef1x+f2(x)ef2x |
| f1(x)+f2(x) |
| f1(x)ef1x+f2(x)ef2x |
| f1(x)+f2(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com