
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,若 ![]() ,则
,则 ![]() = .
= .
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,当
,当![]() 时,恒有
时,恒有![]() .当
.当![]() 时,
时, ![]() .
.
(Ⅰ)求证: ![]() 是奇函数;
是奇函数;
(Ⅱ)若![]() ,试求
,试求![]() 在区间
在区间![]() 上的最值;
上的最值;
(Ⅲ)是否存在![]() ,使
,使![]() 对于任意
对于任意![]() 恒成立?若存在,求出实数
恒成立?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=log2x,g(x)=2log2(2x+a),a∈R
(1)求函数f(x)的解析式;
(2)若对任意x∈[1,4],f(4x)≤g(x),求实数a的取值范围;
(3)设a>﹣2,求函数h(x)=g(x)﹣f(x),x∈[1,2]的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:函数f(x)= ![]() (a>0且a≠1).
(a>0且a≠1).
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)判断函数f(x)的奇偶性,并加以证明;
(Ⅲ)设a=![]() ,解不等式f(x)>0.
,解不等式f(x)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
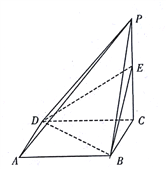
【题目】如图,已知四棱锥![]() 中,底面
中,底面![]() 是边长为1的正方形,侧棱
是边长为1的正方形,侧棱![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 是侧棱
是侧棱![]() 上的动点.
上的动点.
(1)求四棱锥![]() 的表面积;
的表面积;
(2)是否在棱![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 平面
平面![]() ;若存在,指出点
;若存在,指出点![]() 的位置,并证明;若不存在,请说明理由.
的位置,并证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在不为零的常数![]() ,使得函数
,使得函数![]() 对定义域内的任一
对定义域内的任一![]() 均有
均有![]() ,则称函数
,则称函数![]() 为周期函数,其中常数
为周期函数,其中常数![]() 就是函数的一个周期.
就是函数的一个周期.
(1)证明:若存在不为零的常数![]() 使得函数
使得函数 ![]() 对定义域内的任一
对定义域内的任一![]() 均有
均有![]() ,则此函数是周期函数.
,则此函数是周期函数.
(2)若定义在![]() 上的奇函数
上的奇函数![]() 满足
满足![]() ,试探究此函数在区间
,试探究此函数在区间![]()
内零点的最少个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了调查喜欢语文学科与性别的关系,随机调查了一些学生情况,具体数据如表:
调查统计 | 不喜欢语文 | 喜欢语文 |
男 | 13 | 10 |
女 | 7 | 20 |
为了判断喜欢语文学科是否与性别有关系,根据表中的数据,得到K2的观测值k= ![]() ≈4.844,因为k≥3.841,根据下表中的参考数据:
≈4.844,因为k≥3.841,根据下表中的参考数据:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
判定喜欢语文学科与性别有关系,那么这种判断出错的可能性为( )
A.95%
B.50%
C.25%
D.5%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com